座標平面における4つの領域
原点とx軸、y軸
『原点(origin)』と呼ばれる、ある点Oを基準として、その点に水平な直線を『x軸(x axis)』、垂直な直線を『y軸(y axis)』と言う。
普通、x軸は原点より右側がプラス、y軸は原点より上側がプラス領域となる。
そういうx軸、y軸で、適当な点の位置を示せるような平面を『座標平面(Coordinate plane)』と言う。
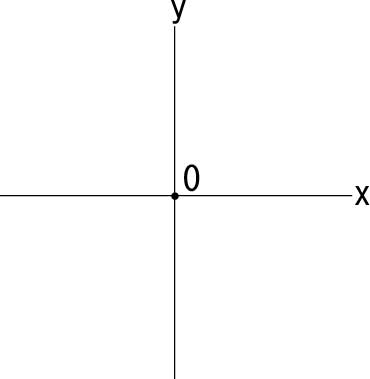
座標平面において、ある点Pの位置を示す場合、その点から、x軸に伸ばした線が交差する点の数値をx座標。
同じように、点Pからy軸に伸ばした線が交差する点の数値をy座標とする。
そうして、点Pの位置を「x、y」というように表せる。
第一象限〜第四象限
平面座標では、十字形となっている、ふたつの軸によって区切られた4つの領域がある。
xもyも、その座標の数値がプラスとなる領域を、『第一象限(First quadrant)』と言う。
そこから4つの領域は、反時計回りで、第二象限、第三象限、第四象限となる。

三角比から三角関数へ
角度に関する関数式
『三角比(Triangular ratio)』は決まっている特定の数値。
 sin、cos、tanは何を表すか?「三角比の基本」
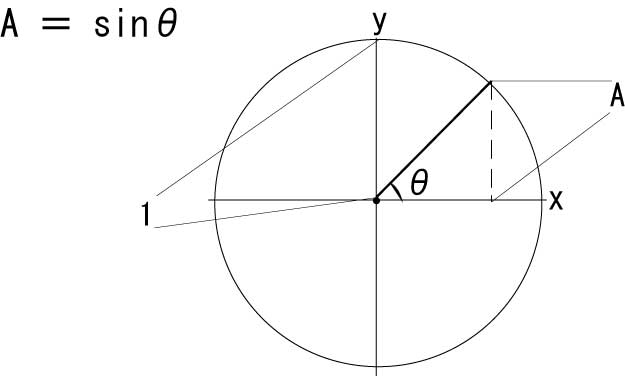
sin、cos、tanは何を表すか?「三角比の基本」
上記の(1)の数式は、角度θ(シータ)の値によって、三角比の値Aが決定する関数式である。
単位円。弧度法。ラジアン表記
関数を調べるには、その変化を座標平面上に書くのがよいが、一般的な関数と、同じような座標平面上に、式(1)を書くのは無理である。
例えば、式(2)のような関数を表すような座標平面のx軸は、長さの変数で表すが、(1)の場合は、θは角度であり、長さに変換するのが無理なため。
角度の変数を表すものとして、半径によって変わる弧の長さが考えられる。
つまり、半径の長さが1の円を想定し、角度の変数をその中心角として、考えるのだ。
そのように使う円を『単位円(unit circle)』と言い、単位円の弧の長さで、角の大きさを表す方法を、『弧度法(circular measure)』と言う。
 正弦定理、余弦定理の求め方、三角形いろいろ「三角比の応用」
正弦定理、余弦定理の求め方、三角形いろいろ「三角比の応用」
半径1の円周の長さは2πとなる。
弧度法では、角度により決定する関数を、
360° = 2π rad
を基準として
180° = π rad
90° = π/2 rad
270° = 3π/2 rad
225° = 5π/4 = rad
300° = 5π/3 = rad
などというように表現する。
radの読み方は「ラジアン(radian)」であり、ラテン語のradius(半径)からきている。
この記号はまた、省略される事が多いという。
サイン、コサインの波
動経の回転。180、360以上の角度
弧度法を用いる事で、考えにくい、sin180以上の数値も定義しやすくなる。
弧度法における半径は、角度の大きさによって、くるくると回転するかのように動く。
その半径を、『動経(radius vector)』と言う。
普通、動経はx軸のプラス側と重なった状態を角度θが0の初期状態として定義する。
そこから、角度が変わる事で行われる回転は、反時計回りがプラス方向、時計回りがマイナス方向と定義する。
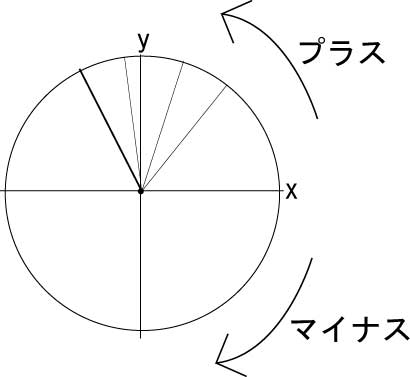
角度が変化して、動経が最初にy軸のプラス側と重なったなら、それは角度θが90になった事。
逆に動経が最初にy軸のマイナス側と重なったなら、それは角度θが-90になったという事。
動経がプラス方向の回転を続け、x軸のプラス側に戻ってきたなら、それは、角度θが360に達したことを意味している。
回転を二周目に突入させれば、360以上の角度も定義出来る。
二周目で動経がy軸のプラス側と重なった時、角度θは450であり、再びx軸のプラス側に戻ってきた時は、720という訳である。
今は何周目かの記述、一般角
ところで、動経がy軸のプラス側と重なっていたとして、それは、角度θが90である事を確実に示しているとは限らない。
もしθが90なら、動経は1/2πだけ動いた事なる。
しかし、θは450、つまり動経は1/2π+2π動いてるかもしれない。
あるいはθは810、動経は1/2π+4π動いているのかもしれない。
そこで、通常、動経の位置を表す場合、y軸のプラス方向に重なっているなら、以下のように表す。
nは当然、何らかの整数である。
式(3)を、『一般角(general angle)』と言う。
ループする周期関数
弧度法を用い、sinの関数式と同じように、cosやtanも関数として定義出来る。
そうして定義された延々ループする関数が、『三角関数(trigonometric function)』という訳である。
また、そういう、一定周期を、繰り返す関数を、『周期関数(periodic function)』と言う。
サインカーブ、正弦曲線。コサインカーブ、余弦曲線
動経が1の場合、単位円の円周上の点pを、(x、y)のように表すなら、(cosθ、sinθ)となる。
また、sinもcosも、180(2π)を境目として、数値がループする。
180から360までの範囲は、
sin(180 + θ) = -sinθ
cos(180 + θ) = -cosθ
となる。
以上をふまえ、y = sin xのグラフを描くと、π、2πごとに、山と谷を繰り返す、無限に続いていく一定の波の記述となる。
そのようなy = sin xを表す波を『サインカーブ(正弦曲線)』と言う。

同じように考え、y =cos xのグラフを描いたら、やはり似たような波の記述となるが、リズムは同じでも、始まりの数値が異なる。
その波は、サインカーブに対して、『コサインカーブ(余弦曲線)』と呼ばれる。
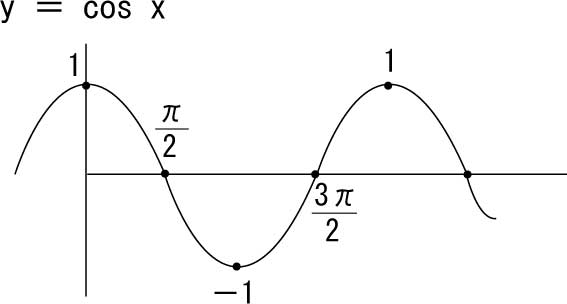
コサインカーブとサインカーブを比較した場合、単にサインカーブをx軸方向にπ/2ズラしたものが、コサインカーブである。
この事から、
sin(π/2 – θ) = cosθ
cos(π/2 – θ) = sinθ
である事も明らかであろう。
周期。振幅
周期関数において、その数値の振れ幅を『周期』と言うが、三角関数のsin、cosは、周期2πの周期関数という事になる。
さらにグラフにおける従属変数(dependent variable)、つまりy = sin xにおけるyにあたる数値の、0を基準とした差の大きさを『振幅(amplitude)』と言う。
サインカーブ、コサインカーブは、yの値が1から-1までの数をぐるぐるしているから、sin、cosの振幅は1という事になる。
点対称な奇関数。線対称な偶関数
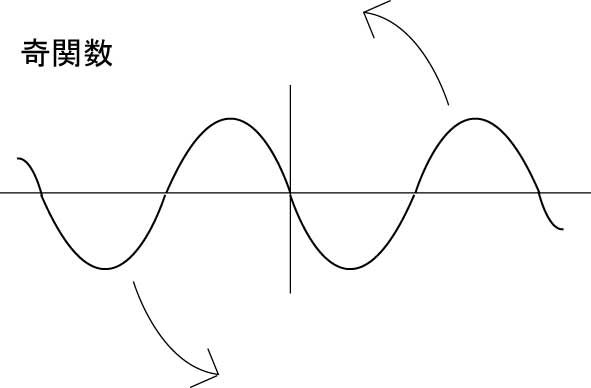
sin のグラフを見てみると、原点を中心として、y軸の右側部分を180°回転させたら、y軸の左部分とぴったり重なる。
そのような、ある点Pを中心に、180°回転させた時に、左右が重なる図形を、「点Pを中心とする点対称な図形」。
そして、グラフを描いた時に、原点を中心に点対称になっているようか関数を『奇関数(odd function)』と言う。
cosのグラフは、y軸でグラフを折り曲げた場合に、左右が重なる。
そのような、ある直線Lで折り曲げた時に、左右が重なる図形を、「直線Lに関する線対称な図形」と言う。
そして、グラフを描いた時に、y軸に線対称になっているような関数を『偶関数(even function)』と言う。
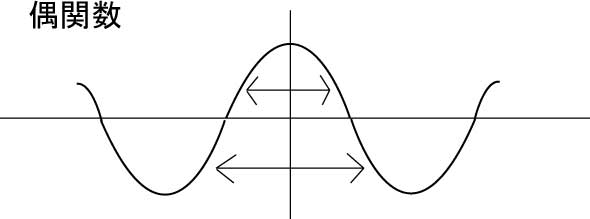
つまり三角関数の、sinは奇関数、cosは偶関数である。
振動、波の大きさと速さ
y = 2sin x
について考えてみる。
これは単位円でなく、動経の長さが2である円におけるサインカーブになる。
どうなるかというと、これは振幅が2になる。
y = 35sin x
なら、振幅は35になる。
y = A(sin x)
のようなサインカーブが何かの振動だとするなら、Aは、その振動の大きさとなる。
y = sin 2x
はどうだろうか。
これは、y = sin xに比べると動経の回転速度が上昇している。
周期が大きくなっているという事でもある。
y = sin xの点Pが円を一周する頃には、y = sin 2xの点Qは円を二周している。
つまり周期がπになっている。
y = sin Bx
のようなサインカーブの振動においては、Bは振動の速度である。
まとめて一般化すると、sinは、
y = A(sin Bx)
振幅A、周期Bの周期関数となる。
もちろんcosも、似たような感じに考える事が出来る。
最低限知っておいても損はない事
三角関数は、三角比が基礎にあるから、まるで図形の領域の関数のようだが、実際には、波や、波として表せれるものと関連が深い。
つまり、波として考えられる現象などの解析に、それが使われることもあるのである。
サインカーブの一般式はy = A(sin Bx)は、Aが波の大きさ、Bが波の周期の早さと考える事が出来る。
その事実を知る事自体は、数学が苦手な人でも、わりと簡単に理解出来るであろう。
それだけ知っておいても、案外役に立つ事もあると思う(創作とかでは特に)。