サイン、コサイン、タンジェント。直角三角形の三角比は何に使うのか
サイン、コサイン、タンジェントと呼ばれる、いわゆる三角比というやつは、直角三角形における決まりごとである。
ただし、これ自体が、直角三角形以外にも、かなり応用のきく便利なものである。
なぜならこの世界というのは、形で成り立っているからだ。
四角の形を想像してみればいい。
それを線で上手く切ったら、二つの直角三角形になる。
同じように、たいていどんな形でも、上手く切ったらいくつかの直角三角形となる。
これは物の形に限った話でない。
例えば、何かが移動した経路を示す線なども、直角三角形の一辺として考えることができる。
物理の数式でも、三角比というのがよく利用されるのは、主にこのような事情のためである。
物事を形に当てはめて、それを直角三角形にして、後は三角比で考えるという順序が、わかりやすいためだ。
tan。タンジェント
二つの三角形の対応する辺が全て平行なら、それらは互いに相似である
数学における証明とは、すでに知られている事から、新たな結果を導くこと。
古代ギリシャの哲学者タレス(紀元前624〜546)は、学んだ数学の知識を用いて、ピラミッドの高さを測定し、エジプトのアマシス王を驚かせたと伝えられている。
タレスが知っていた事とは、「二つの三角形の対応する辺が全て平行なら、それらは互いに相似である」という事。
相似の記号∽。△ABC∽△Abc
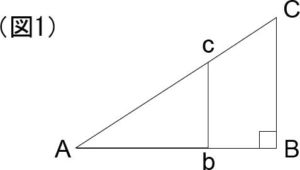
対応する辺が全て平行な三角形とは、重ねた時に、三角形を構成する三つの辺が、全てズレずに重なるような二つの三角形のこと。
例えば「図1」の「三角形ABC」と「三角形Abc」のような二つの三角形である。
相似とは、「対応する、それぞれの辺の長さの比率が等しい」ということである。
例えば図1のような、相似な二つの三角形においては以下のような関係が成り立つ。
「AC/Ac = BC/bc = AB/Ab」
つまり「辺AC」の長さが「辺Ac」の2倍だとするなら、「辺BC」は「辺Bc」の2倍、「辺AB」は「辺Ab」の2倍になるわけである。
二つの図形が相似である事を示す場合、基本的には記号∽を使う。
三角形ABCと、三角形Abcが相似ならば、「△ABC ∽ △Abc」というふうに書く。
∽は「Similar(相似)」のSを横にした記号。
読み方がいるなら、別に「相似」と読んでもいいし、クールに「シミラル」と読んでもいいと思う。
影の長さから、ピラミッドの高さを計算する
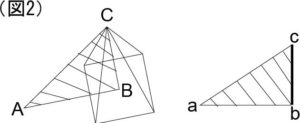
タレスは、ピラミッドの高さと、ピラミッドの底の中心からの影の長さを「隣辺(Cathetus。直角に接する辺)」に見立て、直角三角形ABCを想定。
また、適当な棒と、その影を隣辺にして、相似の直角三角形abcを作ったとされる。
それで、例えばピラミッドの影の長さ(辺AB)が100mで、棒の影の長さ(辺ab)が1mだったとする。
そしたら、「ABC ∽ abc」より、ピラミッドの高さは、棒の長さの100倍だとわかる訳である。
直角三角形の対辺/隣辺
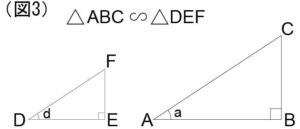
図3のような、直角三角形ABCにおいて、直角と向かい合ってる辺ACを「斜辺」。
他二つの辺を「隣辺」というが、角aや角bと向かい合う隣辺を「対辺」ともいう。
つまり、図3の三角形ABCでは。角aからみて、辺ACが斜辺、辺ABが隣辺、辺BCが対辺となる。
ここで非常に重要なことがある。
それは、相似な二つの直角三角形において、「対辺/隣辺」の数値が一定であること。
二つの直角三角形の大小は関係なくだ。
つまり図3のように、△ABC ∽ △DEFであるなら、「BC/AB = EF/DE」となるわけである。
このような直角三角形の対辺/隣辺を「tan(タンジェント)」という。
例えば図3の直角三角形ABCのBC/ABは、「tan a」などという。
また、△ABC ∽ △DEFであるから、「tan a = tan d」となる。
例えば図3において、ABの長さが5。
BCの長さが4とする。
つまり「tan a = 4/5」
この時、必ず「tan d = 4/5」になるのである。
例えば、「tan d = 2/2.5 = 4/5」になるのかもしれないし、「tan d = 8/10 = 4/5」になるかもしれない。
いずれにしても、結局4/5というわけである。
距離と角度とtan
ところで、tanは、三角形の大きさには左右されないが、角度には左右される。
例えばtan aの数値は、角aによって決定する。
普通に、いろいろ角度の場合のtanの表もあるし、関数電卓でも確認出来るが、記憶力に自信があるなら、暗記するのもよいかもしれない。
また、tanの対辺/隣辺の、隣辺を1とした場合、対辺/1なので、つまり、tanは、「隣辺を1とした場合の対辺」とも定義出来る。
つまり、どこかの(塔とか山とか、何でも)高さを求める場合は、その高さの何かから適当な距離をとって、距離を隣辺、高さを対辺の直角三角形を想定する。
そして、その想定した直角三角形と相似で、かつ、隣辺が1の直角三角形を書けばよい。
例えば、目標物からの距離を100mでとったなら、隣辺を1mにする。
また、対辺と向かい合う角が20°だとすると、目標物の高さは、「tan20 × 100」となる。
ちなみにtan20は0.3639702342…である。
距離は測ればよいし、角度は仰角(ぎょうかく。目線を真っ直ぐにしてる場合の、見上げた角度)か、俯角(ふかく。見下ろす角度)でいい。
その場合、出てくる答は、自分の目線までの高さを、引いた数である事に注意する。
sin、cos。サイン、コサイン
正弦、余弦、正接
相似な複数の三角形において、tanは、対辺/隣辺である。
これと同じように、相似な直角三角形において、「対辺/斜辺」。
それに「隣辺/斜辺」もまた、三角形の大きさに関係なく一定の数値となる。
直角三角形の、対辺/斜辺を「sin(サイン)」、隣辺/斜辺を「cos(コサイン)」という。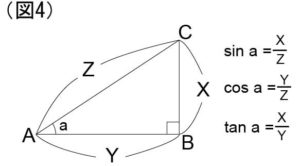
例えば、図4で言うなら、三角形ABCのtan a、sin a 、cos aは、角aの大きさのみで決定するわけである。
相似な直角三角形において、決まっているこのsin、cos、tanという三つの比を、「三角比」という。
また、sin、cos、tanは「正弦(せいげん。sin )」、「余弦(よげん。cos)」、「正接(せいせつ。tan)」とも呼ばれる。
図4のような直角三角形において、また隣辺を1とすると、「tan a = x(対辺)」となるように、斜辺を1とすれば、「sin a = x」、「cos a = y(隣辺)」となり、tanと同じような使い方も出来る。
0と90をどう定義するか。tan90はなぜないか
sin0 = 0
sin30 = 0.5
sin60 = 0.866025403784
sin90 = 1
cos0 = 1
cos30 = 0.866025403784
cos60 = 0.5
cos90 = 0
tan0 = 0
tan30 = 0.57735026919
tan60 = 1.732050807569
tan90 = none
つまりtan90はない。
0や90などおかしくも思えるかもしれないが、例えば角度θが0の時、斜辺Aと隣辺Bは重なって、同じ長さ、そして対辺Cは0という、潰れた三角形を想定する。
sin0 = 0(対辺/斜辺。0である対辺が分子にくる)
cos0 = 1(隣辺/斜辺。隣辺と斜辺が同じ長さ)
tan0 = 0(対辺/隣辺。sinと同じ)
θが90の場合は、今度は、斜辺と対辺が重なって、(現実には絶対ありえないような)潰れた三角形を想定する。
また、この場合、対辺と斜辺の長さは「無限」になる。
sin90 = 1(対辺と斜辺が同じ長さ)
cos90 = 0(分子となる隣辺が0)
tan90 = none(分子が無限になる)
90を超える場合。三角関数への繋がり
sin0 = 0
sin45 = 0.707106781187
sin90 = 1
sin135 = 0.707106781187
sin180 = 0
cos0 = 1
cos45 = 0.707106781187
cos90 = 0
cos135 = -0.707106781187
cos180 = -1
tan0 = 0
tan45 = 1
tan90 = none
tan135 = -1
tan180 = 0
0や90に続いて、さらにその上の直角三角形(なのかどうかもよくわからない何か)はあると定義される。
89までの角を「鋭角」、90の角を「直角」というのに対し、91から180までの角は「鈍角」と呼ばれる。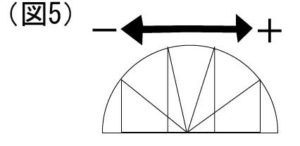
直角三角形が鈍角の領域になると、隣辺がマイナスになったと考える。
つまり三角比は、sinが「対辺/斜辺」、cosが「隣辺/斜辺」、tanが「対辺/隣辺」なので、cosとtanの数がマイナスとなる。
また、鈍角領域で、潰れた180の直角三角形においては、対辺は潰れ0となる。
斜辺と隣辺は重なるが、隣辺はマイナスである。
よって、以下となる。
sin180 = 0
cos180 = -1
tan180 = 0
このような考え方は、円の中で直角三角形をループさせることによって、永遠に続けることができる。
円を一周するごとに数値はひたすら繰り返すので、それはひたすらに繰り返す波を表す関数として使用できる。
そうしたものが、「三角関数」と呼ばれるものである。
巨大球体の半径を三角比で計算する方法
三角比を使えば、 例えば地球のような、自分が立っている惑星の 半径を計算することができる。
例えば惑星の半径を「R」とする。
まずは、高さ5000mの塔に登ってみる。
そこから水平線までの俯角を測り、それは10°だった。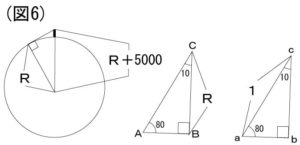
図6のような直角三角形ABCを想定する。
それと相似で、かつ、斜辺が1の直角三角形をabcを想定。
そしたら三角比より、「R = sin80 × (R+5000)」となる。
さらに、R = sin80 × R + sin80 × 5000
R – sin80 × R = sin80 × 5000
R(1 – sin80) = sin80 × 5000
R = sin80 × 5000/1 – sin80
上記の最後の式に、「sin80 = 0.984807753012」を代入すると、「R = 324115.2391051424」
つまり惑星の半径は=324115mほどとなる。
また塔の上から水平面までの距離ABも、上記の半径と、三角比を使い、導ける。
その距離は図5の直角三角形からして、
AB = cos80 × (R+5000)
R = 324115
cos80 = 0.173648177667
AB = 57150.2199928518
つまり塔の上からの水平線の距離は57150mくらいになるわけである。
三角比のふたつの基本公式
直角三角形の角(∠)θにおける三角比は、以下
sinθが「対辺/斜辺」
cosθが「隣辺/斜辺」
tanθが「対辺/隣辺」
という事は、∠θの直角三角形の斜辺を1とすれば、以下
sinθが「対辺」
cosθが「隣辺」
tanθが「sinθ/cosθ」
また、直角三角形の斜辺cの長さと、対辺aと隣辺bの関係が、![]()
になるという、「ピタゴラスの定理」より![]()
となる。
なんだかおかしく思えるかもしれないが、普通、上記の式は、![]()
と書く。
これらは、三角比の基本公式と呼ばれるものである。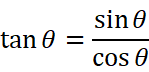
![]()




