三角比。sin、cos、tan
 sin、cos、tanは何を表すか?「三角比の基本」
sin、cos、tanは何を表すか?「三角比の基本」
直角三角形において、「対辺/斜辺」がsin、または正弦。
「隣辺/斜辺」がcos、または余弦。
「対辺/隣辺」がtan、または正接。
大きさがどれだけ違おうとも、相似でさえあれば、共通した比となる、これらを「三角比(Triangular ratio)」と言う。
また、以下のような基本公式がある。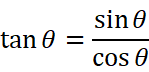
![]()
正弦定理の証明
二つの旗と、船も浮き輪もなしの泳げない人
旗が一本立ってたとする。
そして、あなたは泳げないし、船や浮き輪もないとする。
さらに川をはさんだ向こう岸に、また別の旗が立てられていたとする。
二つの旗の距離がどれだけか、あなたに測る術はあるか?
とりあえず、こちら側の旗から30mの距離に棒を立てる。
そしてその棒と、二つの旗で、三角形abcを想定。
さらに角度を測ってみると、角cが76°で、角aが59°。
さらに点cから線をひき、abcを、二つの直角三角形bcdとacdに分割。
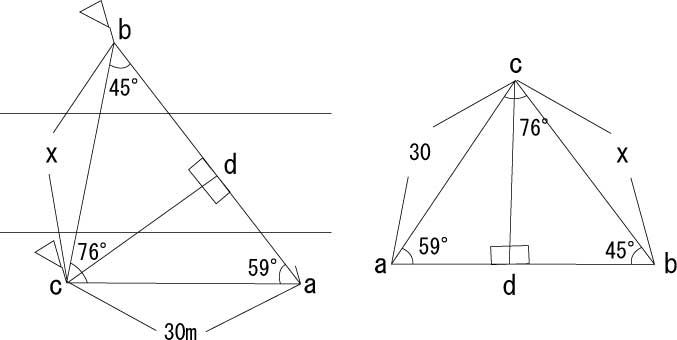
求めたいのは辺bc、つまり長さxの数値。
とりあえず二つの直角三角形に共通する辺cdの長さは、
sin59 × 30
あるいは、
sin45 × x
で求められる。
つまりは、
sin59 × 30 = sin45 × x
である。
ここから、
x = sin59 × 30 ÷ sin45
また、
sin59 = 0.857
sin45 = 0.707
なので、
x = 0.857×30÷0.707 = 36.364
このようにして、知りたかった、二つの旗の距離は、だいたい36.364mぐらいだとわかる。
というように、ある三角形の角がわかってて、かつ辺ひとつの長さがわかってるなら、直線をひいて、二つの直角三角形を作り、sinを使う事で、三角形の残りの辺の長さを算出できる。
二つの直角三角形のパターンと、それぞれのsin
三角形を区切り、二つの直角三角形にする直線は三パターン考えられる。
三つの頂点のどれから線をひくかの違いである。
また、ひかれた線は、二つ直角三角形の共通の一辺となる。
では仮に、△ABCを二つの直角三角形にわけるとする。
また△の三つの辺に関して、
辺AB = x
辺BC = y
辺CA = z
さらに、ある辺と対面する頂点から、直線を繋げた場合に、二つの直角三角形が出来るような、辺上の点をD、E、Fとする。
頂点Aから繋がるのが、D。
Bから繋がるのがE。
Cから繋がるのがF。
このような三角形において、例えば頂点AからDへと直線をひいた場合、 直角三角形ABDとACD ができる。
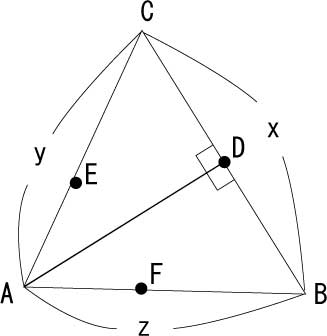
この時、二つの直角三角形の共通の辺であるADに関して、
sinB × z = sinC × y = AD。
つまり、
sinB × z = sinC × y
y / sinB = z / sinC(1)
を導ける。
同じように、BEをひいた場合、 二つの直角三角形の共通の辺であるBEに関して、
sinA × z = sinC × x = BE
よって、
x / sinA = y / sinC(2)
さらに直角三角形ACFとBCFの場合は、
sinA × y = sinB × x = CF
x / sinA = y / sinB(3)
(1)〜(3)より、
x / sinA = y / sinB = z / sinC
という事がわかる。
この平面上では三角比は決まっている
その性質に関して証明されてて、さらにあらかじめ算出された数値表があるならば、sinのような三角比を使うのに、直角三角形を作る必要すらない。
例えば10mの棒があったとする。
それで5mを測りたい時、わざわざ棒を半分にする必要はないであろう。
棒の半分が5mだということがわかっているなら、その半分までの長さを測ればよいだけの話である。
それと同じような事なのだ。
三角形に直線を引いて、二つの直角三角形となることがわかるのなら、どの角度にも三角比の値を定義して、問題はない。
一般式の文字のややこしさ。少なすぎるアルファベット
それと、一般式に使われるアルファベットなどの文字について、惑わされてはいけない。
どの文字を使うかなんて、時代や場所によって変わってきたし、究極的には、使う人の好み次第である。
だいたいアルファベットなんて、大した数もないのに、一般記号として使うなんてことが、そもそもバカげてると言えなくもない。
もし数学が、日本や中国でのみ、進化してきたものだったなら、我々は、大量に存在する、漢字という記号を使えたかもしれない。
そしたら、実際にそうなっているように、別の意味の記号に、同じアルファベットを使ったりなどという事を避けることができたはずである。
漢字というのは、かなり多いし、いざとなったら手軽に作れるし。
一万年後くらいには、数式記号として、真面目に漢字を使うのが主流になってるかもしれない。
外接円。中心角。円周角。正弦定理
三角形ABCかあって、 2つの頂点それぞれと向かい合う辺をx、y、z。
頂点A(角度A)と向かいあう辺をx。
頂点B(角度B)と向かいあう辺をy。
頂点C(角度C)と向かいあう辺をz。
これに関して、我々は今や、
x / sinA= y / sinB = z / sinC(4)
である事が知っている。
また、三角形の三つの頂点と接する円を、「外接円(Circumscribed circle)」と言う。
ある円があって、その中心点をP。
その円の半径をRとする。
円上に適当にとった二つの点にはさまれた円の部分を「弧」と言うが、適当に点HとJをとって、弧HJを作る。
そのような弧HJにおいて、角HPJを、弧HJにおける「中心角(Central angle)」と言う。
そして、弧HJにない円周上の適当な点Kやkからなる、角HKJや角HkJを、弧HJにおける「円周角(Circumferential angle)」と言う。
実は、中心角と円周角について、ある弧に対しての、その弧以外のどこにとった点を使っても、作った円周角は全て等しい。
さらに、
中心角 = 円周角 × 2
である。
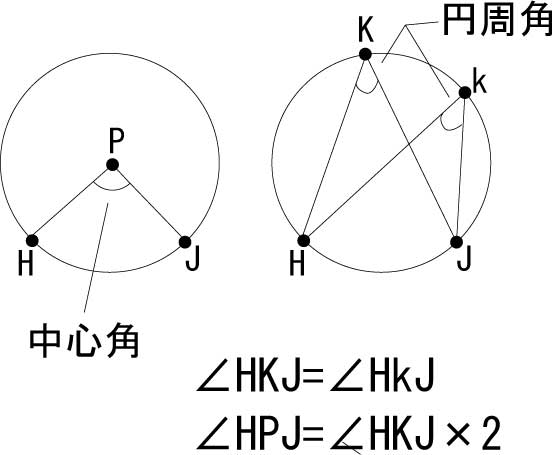
ところで三つの点HPJが一直線に並んでる場合(つまり直径をなす場合)、中心角は180なので、円周角は90、つまり直角となる。
三角形ABCとその外接円について考えてみる。
角Aと向かいあう辺をx、Bと向かいあう辺をy、Cと向かいあう辺をz。
外接円の中心をP、半径をRとする。
直線APDを作るような点Dを外接円上にとり、直角三角形ABDを想定。
ABDは斜辺が直径2Rの直角三角形なので、
z = sinD × 2R
sinD = z / 2R
が成り立つ。
また、二つの三角形それぞれにおける、角Cと角Dは、いずれも、弧ABの円周角でもあるので、
∠C = ∠D
である。
よって、
sinD = sinC = z / 2R
2R = z / sinC(5)
(4)と(5)より、
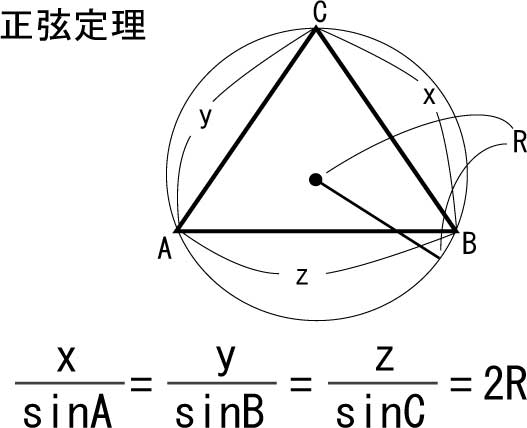
となるのである。
これは「正弦定理(Sine theorem)」と呼ばれる。
正弦定理の使い方
正弦定理を用いれば、ある三角形において、二つの角と一辺の長ささえわかれば、残りの辺の長さを求められる。
三角形の外接円の半径もわかる。
また、ある三角形の一つの角と、外接円の半径さえわかれば、その三角形の判明している角の、対辺が導き出せる。

余弦定理の証明
正弦定理が使えない状況
A地点とB地点それぞれにある二つの旗の距離を調べてみたいが、間に巨大な岩があって、直接距離を測ることができない。
そこで、AB両地点に立つ旗が、両方とも見えるC地点を決めて、三角形ABCを想定した。
A地点からC地点までの長さが39m。
B地点からC地点までの長さが36m。
角Cが69°。
しかし、A地点とB地点のそれぞれからは、間の岩が邪魔で、角度も測れない。
角度が一つしかわかっておらず、外接円の半径もわかっていないので、正弦定理は使えない。
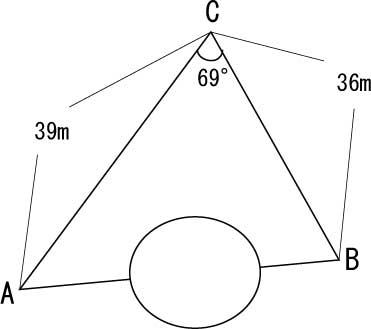
とりあえず、 三角形ABCの頂点Aから直線をひき、BC上の交差点をDとして、直角三角形を二つ想定。
片方の直角三角形ACDは、斜線が39とわかるから、
AD = sin69 × 39 = 36
CD = cos69 × 39 = 14
BD = 36 – cos69 × 39 = 22
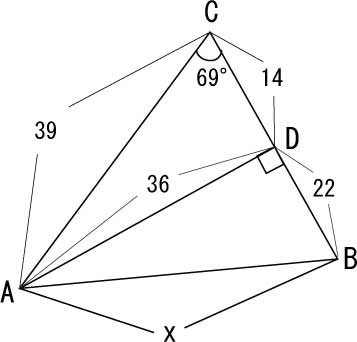
これで直角三角形ABDの二辺の数がわかったから、後はピタゴラスの定理により辺AB、すなわちA地点とB地点の距離は算出できる。
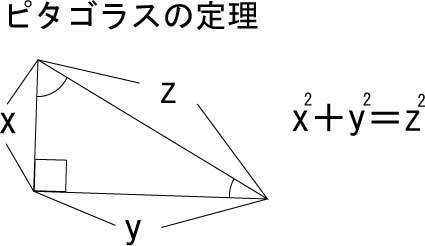
22^2 + 36^2 = 1780
√1780 = 42
つまりA、B地点の旗の距離は42mである。
sin、cosを上手く使えば、二つの辺の長さと一つの角度からでも、このように、もう一つの知らない辺の長さを計算することもできる。
余弦定理
また、三角形ABCかあって、2つの頂点それぞれと向かい合う辺をx、y、z。
頂点A(角度A)と向かいあう辺をx。
頂点B(角度B)と向かいあう辺をy。
頂点C(角度C)と向かいあう辺をz。
とする。
この三角形の頂点Cから辺ABに直線を下ろし、やはり交点をDとして、直角三角形を二つ作る。
二つの直角三角形に共通する辺CDはwとし、辺ADはv、辺BDはuとする。
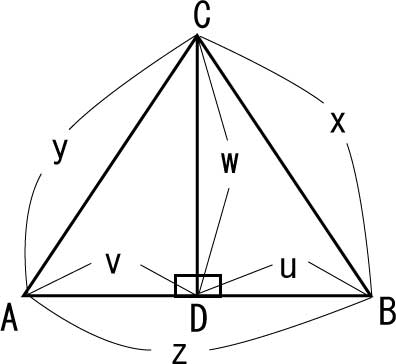
直角三角形ACDにおいて、
w = sinA × y
v = cosA × y
よって、
u = z – cosA × y
さらに、
x^2 = (sinA × y)^2 + (z – cosA × y)^2
これを解くと、
x^2 = y^2 + z^2 – 2 × y × z × cosA
また、同じように、
y^2 = x^2 + z^2 – 2 × x × z × cosB
z^2 = x^2 + y^2 – 2 × x × y × cosA
となる。
さらに、上記のような式を少しいじればcosを求める事も出来る。
まとめると、
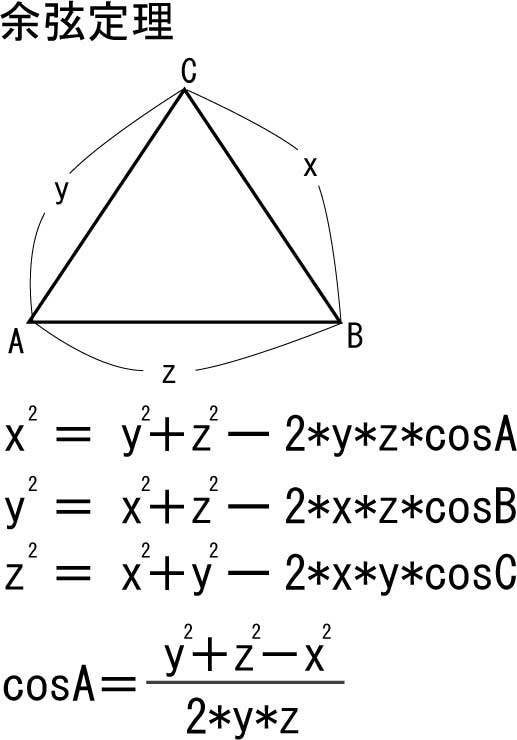
これは「余弦定理(Cosine theorem)」と呼ばれる。
余弦定理の使い方
余弦定理を使うことで、ある三角形において、二つの辺と一つの角から、残りの辺や角などを算出出来る。
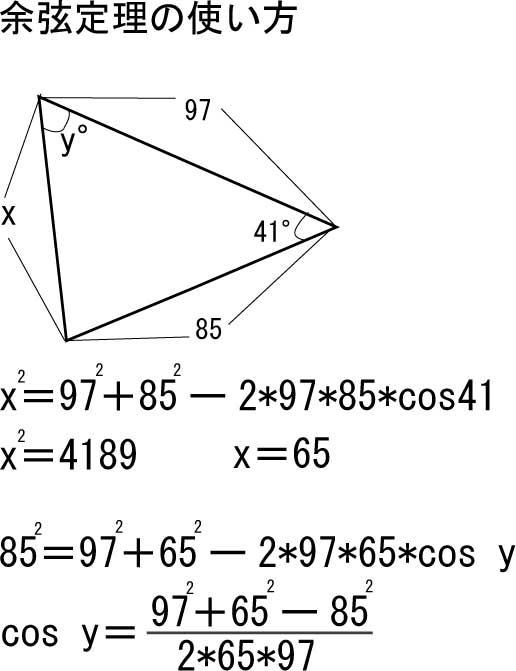
また余弦定理で導いたcosから、三角比の基本公式を使い、sinも導ける。
三角比と面積
sinを使い三角形の面積を求める
二辺とその間の角が分かってれば、三角形の面積はsinで求めることが出来る。
三角形の面積は、「底辺×高さ/2」で求める事が出来る。
三角形を直角三角形二つに区切る線は、その三角形の高さの線でもある。
つまり、高さはsinで、表せれる。
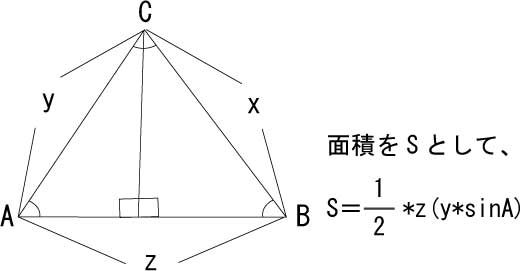
余弦定理とヘロンの公式
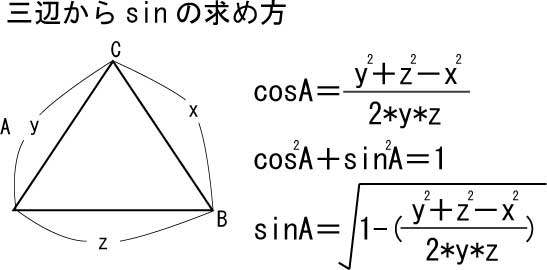
ある三角形ABCに関して、三つの辺の長さ、x、y、zがわかってるとする。
余弦定理からsinを、以下のように算出できる
上記の計算で求めたsinを使い、三角形の面積の計算も出来るし、その式からさらに、三角形の面積を求める便利な公式、「ヘロンの公式」が導ける。
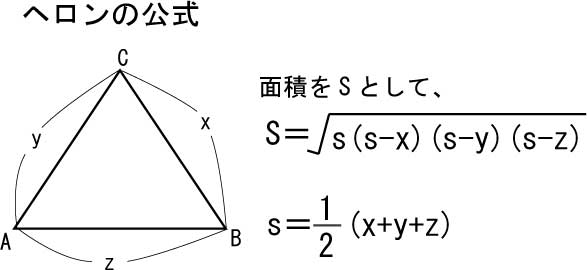
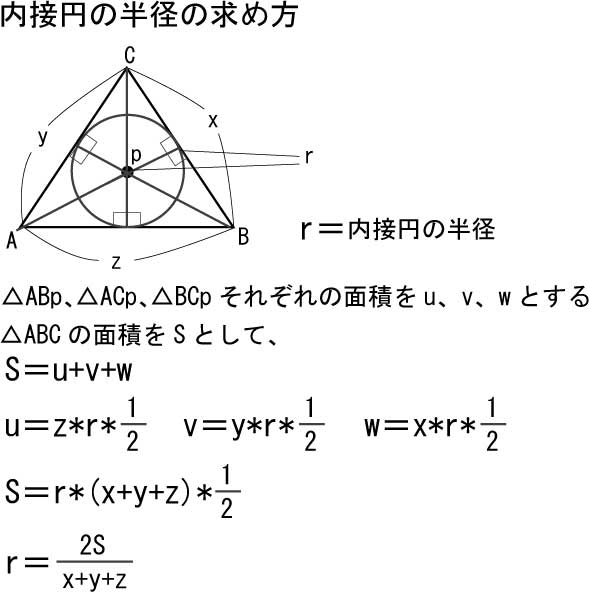
内接円の半径
三角形の三つの頂点と接する外接円に対して、三角形内部で、それぞれの辺に接するように描かれた円を「内接円(Inscribed circle)」と言う。
三角形の内接円の中心点から、それぞれの頂点に直線を引き、三角形を三つに分割する。
そうした場合、内接円が、三つの三角形それぞれの高さとなる。
そこから、以下のように、内接円の半径を求めれる。