「微積分とはどのような方法か？」瞬間を切り取る

微分の方法

リンゴが落ちる時に

　『微積分（びせきぶん）』を発明したとされる数学者アイザック・ニュートンは、一般的には重力理論である「万有引力の定理」の提唱者としてよく知られている。
真実かはかなり怪しいらしいが、ニュートンは木からリンゴが落ちるのを見たのがきっかけで、万有引力のアイデアを思いついたという。
「ニュートン」万有引力の発見。秘密主義の世紀の天才
　そこでこのエピソードにロマンを感じたあなたは、ニュートンの伝記映画を作り、信憑性など気にもせず、その落ちるリンゴの目撃というシーンをクライマックスにしたとする。
それとクライマックスなので、あなたは特に拘り、納得のいくものにするために、落ちるリンゴの速度が異なる様々なパターンを作った事にもする。

　正直、映画の出来はどうでもよいけど、クライマックスシーンの、リンゴの速度パターンごとの違いについて考察する事は、『微分法』の基本を理解するのに役立つと思われる。
「微分積分の関係」なぜ逆か。基本公式いくつか。指数対数関数とネイピア数

一定の直線、変化の曲線

　リンゴが落ちるシーンの一瞬一瞬を静止画として切り取り、並べて比べると、連続的な動きの映像ではわからないだろう、ある事実が明らかになる。

　
　図1のAが「リンゴの落下速度が常に一定の場合の静止画並び」で、Bが「落下速度が徐々に加速している場合」、Cが「落下速度が徐々に減速している場合」である。

　さて、横に並び合う静止画のリンゴを線で繋げてみる。

　図2のように、速度が一定の場合は真っ直ぐの線が、速度が変化している場合には曲線気味の線が現れる。
この曲線は変化速度が一定していないせいであり、加速する変化を捉えにくくする。

変化の瞬間を捉える

　まだ一定のリズムで変化する分にはマシだ。
例えばある瞬間に速度1で動いていたロケットがあったとして、2秒後には速度4、4秒後に16、そして6秒後に36なら、5秒後は多分25だったのだと推測するのは容易い。
一般的な数式で表すなら、t秒後の速度をvとして、
$v=t^2\mathrm{ （1）}$
となるだろう。

　実に簡単だが、不規則に変化速度を変えるものとなるとそうはいかない（しかも現実の物はたいていそうである）
2秒後に11、4秒後に5、6秒後に59になっているロケットが5秒後の時点でどれくらいかを推測できるだろうか？

　これは理屈の上では可能とも、不可能ともいえる。
しかし微分法は、そのような不規則な変化速度すらを正確に導ける事を前提としている。

　その基本原理自体は単純である。
つまり何かが動く時、あるいは変化する時の、その瞬間を捉える。
微分法とはそうした方法である。

区切られた一瞬の真の速度

無限空間のガラクタ

　微積分と万有引力以外にも、ニュートンの発見はいくつもある。
外部から新たに力が加えられない限り、静止している物体は静止を続け、動いている物体は動き続ける、という運動法則も、彼が考えたらしい。

　では天才ニュートンを信じ、他の物質が何もなく、無限に広がる空間に、適当なガラクタをひとつ置いてみるとする。
そして神の力を持って、そのガラクタを軽く押し動かす。
「宇宙プログラム説」量子コンピュータのシミュレーションの可能性
その後はもう何もしない。
するとガラクタはひたすら無限空間の中、一定方向に一定速度で動き続ける事になる。

　速度とは、どれくらいの時間で、どれくらいの距離を移動できるかを示す数値であり、一定なら、移動距離を使用時間で割るだけで求められる。

　もしガラクタが、x時間でyキロ移動したとするなら、ガラクタの速度vは、
$v=\frac{y}{x}\mathrm{ （2）}$
となる。
だがこれは、もちろん一定速度で動くものを対象にする場合である。

変化の割合

　微分では、ある時間における変化度合いこそが重要で、それは「変化の割合」などと表現される。

　変化の割合を表す記号は、通常、距離や量の記号に『’（プライム）』の記号をつけたもの（注釈1）

　例えば、t秒でsメートル走る車の変化の割合はs’となる。

　記号に数字を割り当てた場合は以下のようになる。　
常に一定速度で、3秒で15メートル走る車があるとすると、「t＝3に対して、s＝15、s’＝5」

　量の例としては、発電装置がt秒でfジュールを生成したなら、エネルギーの生成速度という変化の割合はf’となる。
一定の生成率で、10秒で100ジュールエネルギーを生み出す発電装置があるとすると、「t＝10、f＝100、f’＝10」である。

　ではとんだインチキ品で、あらかじめ100ジュール生成されてただけで、一切作動せず10年放置された発電装置の場合はどうなるか。
この場合は「t（秒）＝315360000に対して、f＝100、f’＝0」となる。

時間0、速度0

　とりあえず、実験空間のガラクタに話を戻す。

　例えば神が、空間にデタラメに他の物を配置していったなら、それらの重力の影響が、常にガラクタの速度を不規則に変化させるだろう。
そうなると式（2）は、あまり有効でなくなると考えられる。

　でもわずかな時間の間の速度を考える場合はどうであろう。
例えばガラクタの1時間後の速度は全く予想つかないが、0.1秒後なら、おそらく今とそんなに変わっていないと予想出来る。

　微分法は、この0.1秒をさらに0.01秒、さらに0.001秒と無限に小さくしていく事で、常に変化する速度すら、暴いてしまう。
「無限量」無限の大きさの証明、比較、カントールの集合論的方法
　しかしある瞬間の変化速度とは何か？
仮にガラクタの5時12分の瞬間の速度を知りたいとする。
まず5時11分にガラクタがどこにあって、13分にどこにあったかを調べる。
その2分の間で数式（2）を用いたなら、2時間の間で考えるよりは正解に近い値が得られるはず。
基準とする時間をさらに狭めていけば、値はさらに正解に近づくだろう。

　だが、時間を狭め、それがついに0になった時、我々は何か間違っている事を認めざるを得ない。
なぜなら時間0の間には移動など出来ないから、結果、速度も0となってしまうのである。
しかし実際問題、0でない時間の中で、ガラクタは動いているので、それは絶対にありえない。
　

極限の概念

　そこで数学者は、『極限』という概念を考えだした。

　極限とは、ある値に限りなく近いが、ある値ではない数である。
それはつまり少数を含む全ての数を横並びにした表における、ある値の前後に隣接している数である。

　つまり12分のときの速度を知るには、数字全てを並べた表の、12の前後に隣りあうふたつの数の差を使えば、0でなく、かつ限りなく正確な12分の瞬間速度を導き出せるというわけだ。

実際に瞬間を求める

　では極限を使うというアイデアを武器に、
$y=x^2\mathrm{ 数式（3）}$
について考えてみる事にする（注釈2）
この式によると、x＝1ならy＝1、x＝2ならy＝4、x＝3ならy＝9である。

　数字を比べればわかるように、明らかにyの瞬間ごとの速度、あるいは変化の割合y’は上昇を続けている。
では仮にx＝2の時点の変化速度y’を調べるとする。
xの値1と2の間で、yに3（4-1）の変化があった。
速度の公式である数式（2）に（時間に相当する）数xの差1（2-1）と（距離に相当する）変化3を、共に当てはめると、瞬間速度y’は3となる。
2と3の間では、yに5（9-4）の変化があり、これも同じく数xの差1（3-2）と共に当てはめたら速度y’は5となる。
とするとおそらく2の時点でのy’は、3から5の間の数だと思われる。

　では範囲を狭め、数xが1.9から2の間、2から2.1の間の時のy’を見てみる事にする（注釈3）
数式（3）でxに1.9を代入するとy＝3.61。つまり1.9から2の間の変化は0.39（4-3.61）。
xの変化は0.1（2-1.9）なので、数式2に当てはめ、y’は3.9。
xが2から2.1の間では、y’は4.1となる。
まあ範囲は絞られた。

　では次はさらに範囲を狭め1.999と2.001の間を考えてみる。
出てくるy’は3.999と4.001。
以降はどれだけ範囲を狭めても3.99の後に9の数が増え、4.00の後に0が増えていくだけである。
つまりx＝2の時点でのy’の前後の極限は、3.999……9と4.000………1という事になる。
3.999……9より大きく、4.000……1より小さい数。
それは明らかに4。
つまりx＝2の時点での変化速度y’は4という事になる。

　同じやり方でx＝1の時のy’を求めると、答は2となる。
x＝3の時は、y’＝6。
x＝4の時は、y’＝8となる。

　答は明らかに記号を用いた一般化が可能である。
つまり、数式（3）における瞬間ごとの変化速度y’は常に、
$y<!--FUNCTION\; APPLICATION-->‘=2<!--INVISIBLE\; TIMES-->x\mathrm{ （4）}$
となる（注釈4）

たいていの場合

　極限など考えなくても、単に隣り合う整数の差から導ける速度を取れば答が出ると考えたかもしれないが、これは数式（3）が特殊な場合だからであり、例えば、
$y=x^3\mathrm{ （5）}$
の場合には、その考えは誤った答を導く。

　数式（3）の場合と同じように、極限を用いて瞬間速度を計算すると、その答は、
$y<!--FUNCTION\; APPLICATION-->‘=3<!--INVISIBLE\; TIMES-->x^2\mathrm{ （6）}$
となるが、これは普通に、整数のみを使った計算では導き出せない。

微分の基本数式

極限の記号lim

　極限にも記号がある。
しかも非常に言葉な感じで、limit（限界）のlimである。

　例えばある数xを0に限りなく近づける時には、
$\underset{x\to <!--RIGHTWARDS\; ARROW-->0}{\lim }$
のように書く。
　

1文字が持つ無限の可能性

　実際の瞬間というのは、例えば2からその極限までの距離というのは単に、2＋hでいい。
2＋hは、つまり（hに-0.000……1を代入して）1.999……9にもなるし、（hに0.000……1を代入して）2.000……1にもなるのだから。

　つまり瞬間速度y’は、2と2＋hの間の速度で、かつhが限りなく0に近い時というわけである。
実際に数式（3）に当てはめると、


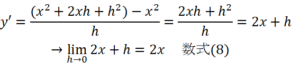
というわけで、実に簡単に答を得られる。

　このやり方で、数式（5）も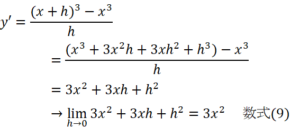

と比較的容易に導ける。

　さらに数式（8）と（9）の答より、あなたはある予測を立てたかもしれないが、多分それは当たっている。

　つまり、

の時は、

となるのである。

空想と推測

この世界はふたつの国だけ

　この世界がたった2つの国、AとBだけで成り立っているとする。
　
　Aの国土の広がり速度をA’、Bの国土の広がり速度をB’とする。
ではこの世界の広がり速度はどのくらいになるのか？
当然この世界はAとBのみから成り立つ世界なので、AとBの国土の広がり速度を合わせた数になる。
つまり世界（A＋B）の変化速度は（A’＋B’）となる。
これは、AとBを何に例えても同じ結論が出る。

　要はこういう事だ。

の時は、

になるわけである。

公式的な用語

　別の数xに左右されるある数yなどを『関数』というが、その瞬間の変化速度を『導関数』という。
すなわち微分とは、関数から導関数を求める事に他ならない。

　さてここでひとつ疑問。
導関数から導関数を導けるか？
普通に導ける。
例えば、

という感じである。

　だが最後の6をどう考えるべきか？
導関数とは、瞬間の変化速度であったはずである。
だが今やその速度y’は常に6という状態。
つまり変化は常に0。
なので最後、6の導関数は0となる。

　微分はこのように、あらゆる変化速度を導関数という形で表すのである。

積分についての話

実は先に開発された積分

　『積分』は歴史的には、微分より早く発明された。
そして積分と微分は、方法を逆にしただけという関係にある。
といってもこれは偶然で、微分は、積分を逆に使うやり方に名前をつけたとか、そういう訳ではない。

　積分と微分は全く別の分野として開拓されたのだが、実は単に裏表の関係だったという訳なのである。

　では積分とはどういうものなのか。　
というと、面積や体積の正確な大きさを図る為の方法である。

円の面積は図れるか？

　紀元前200年くらいに、アルキメデスとかいう、裸で街を走り回るのも平気だったというほど、心の強いお方が、勇気を持ってある難問に挑戦した。

　それは円の正確な面積を図るというもので、アルキメデスは『取り尽くしの方法』というのを使って、まあまあ惜しいとこまでいったらしい。

　そしてその取り尽くしの方法とは、現在の積分にも近い方法だったようである。

　曲線で囲まれた円という図形を正確に図るのは難しい。
直線なら簡単である。
例えば長方形は、単に縦の長さと横の長さを掛け算すればいいだけだ。

　アルキメデスは曲線を大量の直線の集まりとみなし、大量の直線の図形として円を計算した。
現在の積分では、円を大量の細長い長方形の並びの極限として、計算してみるのである。

Δな積分の方法

　ところで極限みたいな僅かな量を表すのにΔ（デルタ）という記号を使うのも、なかなかスタンダードである。
例えば長さxの内の僅かな一部をΔxと書いたりする。
ここからはこれも使う事にする。

　とりあえず、円を大量の長方形に分けた後に、その一本を取り出す。
円の縦軸の長さをS、限界まで分けられた長方形の幅をΔSとするとその取り出した長方形ひとつの面積はSΔS（S×ΔS）となる。
　
　求めたい円の半径の長さをrとすると、縦軸の長さは2rとなる。
そして円の中心点を0とすると、円の端の数値はrで、もう一方の端が-rという事になる。
とすると、rと-rの幅の間の全てのSΔSの合計、つまり和を取れば、円の面積は得られる事になる。
和を表す記号∫（インテグラル）を用いて書くと、

となる。
「取り尽くし法」台形、三角形、円を、積分と極限で求める術
　積分とはこのような方法である。