自然数。整数。分数。無理数。虚数
普通に、
1、2、3……
と続いていく数が『自然数(natural number)』である。
自然数と0、それに
-1、-2、-3……
と続いてく数を、まとめて『整数(integer)』と言う。
1/2とか、5/9とか言った数は『分数(fraction)』である。
0.54とか85.9とかは有限少数。
0.555……とか0.31818……とか、同じ数字パターンがひたすら繰り返されるのは循環少数と言われるが、これら(有限少数と循環少数)は、実質的に、分数と(表記のされ方が違うだけで)同じである。
しかし0.4953735319……と、ひたすらデタラメなパターンで数字が続いていく無限少数は、『無理数(irrational number)』である。
√2やπ(円周率)など、少数表記に変換すると無限少数になってしまう数は全て無理数。
整数と分数はまとめて『有理数(rational number)』と言われ、有理数と無理数はまとめて『実数』と言われる。
そして√-2のように、少数表記に変換する事すら不可能な数が『虚数(imaginary number)』である。
また、実数、虚数をさらにまとめて、『複素数(complex number)』と言う。
1を少数で表すと0.999……?
1は少数で表すとどうなるであろうか?
1.0でもいいかもしれないが、実はほぼ確かなのが、
1 = 0.999……
というもの。
単純に1を3で割ってみると、答は明らかに1/3である。
そして1/3を少数に変換すると、0.333……となる。
0.333……×3 = 0.999……
なので、1は1であり、0.999……でもあるのである。
√2はどの辺りの数なのか
√2のような無理数を評価するには不等号が便利である。
例えば自然数x、yの関係が、
x>y
だったとする。
その場合はまた、
√x>√y
でもある。
そういう風に考えると、すなわち、
√1<√2<√3<√4<√5<……
よって
1<√2<√3<2<√5<……
なので、少なくとも√2と√3は、1以上2以下の数である。
素数。合成数。素因数分解の一意性
ある整数Nを割って何らかの整数nになる時、nをNの『約数(divisor)』と言う。
自然数の内、1とその数自身以外に約数を持たないような数を『素数(prime number)』と言う。
いろいろ議論されがちだが、基本的には、1は素数には含まれない。
また4以上の偶数は全て2で割れるので、2は唯一の偶数の素数である。
素数以外の自然数を『合成数(composite number)』と言う。
合成数には必ず、何らかの素数の積(掛け算)がある。
そしてその、ある合成数を表す、素数のみの数式は、数字の順番を考慮しなければ、必ずひとつしかないとされている。
例えば120を素数のみの数式で表すと
2×2×2×3×5
となる。
そして120を表す素数のみの式は、上記のみである。
また、そういう素数のみの式を『素因数分解(factorization into prime number)』と言う。
さらに、素因数分解の組み合わせが、必ず各数ごとに、ひとつしか存在しない事は、『素因数分解の一意性(uniqueness)』と言われる。
ちなみに、1が素数ならば一意性は崩れてしまう。
また、素数が無限にある事は、すでに紀元前から証明されている。
 「素数とゼータ関数」リーマン予想に晒された架空の実領域
「素数とゼータ関数」リーマン予想に晒された架空の実領域
単項式。多項式。有理式
数が使われてるか、文字が使われてるかは関係なく、ひとつの掛け算で表せられた数を『項(term)』と言う。
項に含まれる、あまり重要でないとされる数や文字は『係数(coefficiewmt)』と言う。
項ひとつのみの式を『単項式(monomial)』と言い、単項式の和(足し算)を『多項式(polynomial)』と言う。
あるいは『整式』
ふたつの多項式の商(割り算)として、書かれた式を『有理式(rational expression)』。
あるいは『分数式(fractional expression)』と言う。
交換法則。結合法則。分配法則
A、B、Cをある数、あるいは多項式として、以下の法則が成り立つ。
『交換法則(commutative law)』
A+B = B+A
A×B = B×A
『結合法則(associative law)』
(A+B)+C = A+(B+C)
(A×B)×C = A×(B×C)
『分配法則(distributive law)』
A×(B+C) = A×B+A×C
(A+B)×C = A×C+B×C
二項定理
指数法則
指数とは当然![]()
などにおけるnである。
それは例えば、nが2なら
A×A
nが5なら
A×A×A×A×A
となるようなものである。
指数がついた数の計算には、『指数法則(exponential law)』というのが成り立つ。
すなわち、![]()
![]()
![]()
である。
パスカルの三角形
![]()
![]()
![]()
というようになるのだが、上記の計算の流れを『二項展開(binomial expansion)』と言う。
そして、二項展開における、各項の係数を『二項係数(binomial coefficient)』と言う。
そしてパスカルの三角形というのがある。
以下のようなものである。
見ての通り、次々枝分かれする数字が、交差する時に足し合わされていくというものである。
この頂点を
n = 0として、二段目から、
n = 1、2、3……
と増えていくのだとする。
それを![]()
のnと同一としたら、三角形のnの段が指し示しているのは、まさしく二項展開の係数となる。
階乗。あるいは奇数のみ、偶数のみの場合
3! = 1×2×3
5! = 1×2×3×4×5
1! = 1
n! = 1×2×3×……×n
というように定義されるのが『(自然数の)階乗(factoral)』と言われるものである。
偶数のみの階乗は
(2n)!!
奇数のみの階乗は
(2n-1)!!
と書かれる。
奇数の方の階乗にて、nが0の場合は、0!!と同じと見なされる。
そして
0!! = 1
とする。
また![]()
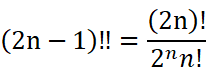
である。
組み合わせと総和の記号を使って
それぞれ異なっているn個のものから、r個を取る組み合わせを、![]()
と書く。
さらに、ある数iに、何らかの数(例えば1)からnまでの数を連続で代入していくという事を表すには、![]()
と書く。
二項係数は、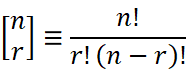
と書かれる。
「≡」は「定義する」というような意味の記号。
そしてその事を踏まえると、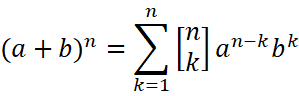
となるのである。
これが『二項定理(binomial theorem)』と言われるものである。




