エウクレイデス、原論。宇宙の幾何的構造を示すとされてた書
教科書的内容
エウクレイデス（ユークリッド）の原論ほど、人類の役に立ってきた書物は、おそらくは存在しない。
なぜ数学を学ぶのか？「エウクレイデスと原論の謎」
それはおそらく、ギリシア幾何学の成果の集大成であり、長きにわたり、多くの人にとって、宇宙の存在に関して、人類に知れる限りを綴った書であった。
原論は全13章。
実のところ、標準的な教科書だったのではないか、と言われるくらいに、驚くべきほどしっかりとした構成となっている。
内容としては主に、第1章が、直線（Straight line）、平行線（parallel lines）、三角形（triangle）。
第2章が面積（area）。
第3章が円（Circle）。
第4章が正多角形（regular polygon）。
第5章が比例（Proportional）。
第6章が相似形（Similar form）。
第7〜9章が整数論（Number theory）や算術（arithmetic）。
第10章が無理数（Irrational number）。
第11〜13章は立体図形（Solid figure）についての内容。
五つの公準
今は、何かの問題に取り組むにあたり、最も基礎的な事を、『公理（axiom）』と言う。
エウクレイデスは原論にて、公理を「一般に真だと認められている事」として、それとは別に、「幾何学を構築する際に、前提として認める事を要請する事」として『公準（postulate）』というのを用いている。
まず初めに、「点とは部分のないもの」とか、「線とは幅のない長さ」とか、いろいろな定義が出される。
そして定義の次に、5つの公準がくるのである。
1、任意の点より任意の点に直線をひける
2、直線は延長できる
3、任意の中心と半径を持つ円を書ける
4、直角はすべて相等しい
5、与えられた直線Lの、上にない、与えられた点Pを通り、どれだけ延長しようとLと交わらない直線が、ただひとつだけ引ける。
まず明らかなのが、第五公準だけ妙に長い。
ある線に対し、ある点を通る平行線は、ひとつしか引けない
原論の第五公準は、つまり、「ある線に対し、ある点を通る平行線は、ひとつしか引けない」という事。
これは確かに基礎的なことと言えるような、かなり当たり前の事にも思える。
しかし、第五公準は、その妙な長さと意味深な内容から、ひょっとするとこれは、他の公準から証明できる類のものではないか、という疑惑が、古くからあった。
そして、そうだとするなら、それはこの原論という本に、公理がダブっているという、明らかな構成ミスがある事を意味している。
それは、原論こそ、全ての幾何学に通ずる最上の書物とされていた時代には、かなりトンデモない事であった。
第五公準問題。平行線問題
第五公準は、他の公準から証明できるのか否か。
『第五公準問題』、あるいは『平行線問題（Parallel line problem）』と言われるこの問題に、多くの数学者が取り組み、そして、答に近づくとともに、様々な事が明らかになっていった。
そういう発見の中で、最も 衝撃的で、かつ重要だったのが、ハンガリーのボーヤイ・ヤーノシュと、ロシアのロバチェフスキーが、ほぼ同時期に導き出した、『非ユークリッド幾何学（Non-Euclidean geometry）』であった。
ちなみに第五公準自体は、結局、ユークリッド幾何学においては、他の公準から導けると証明されはしなかった。
確かにユークリッド幾何学的世界においては、それは公準と言えるようなものであったのである。
ただし1868年頃、ユージニオ・ベルトラミにより、「第五公準は、ユークリッドの他の公準から論理的には独立している」ことは示されている。
双極幾何学。球体幾何学。非ユークリッド幾何学とは何か
ボーヤイ。ロバチェフスキー。ガウス
ボーヤイの父は、平行線問題に一生を費やし、息子には、それには関わらないように忠告したとされる。
しかしボーヤイは結局、父と同じように平行線問題の研究に取り組んだ。
そして彼は、第五公準の通用しない、ある点を通る平行線が複数あるような世界の幾何学を思いついた。
ボーヤイは、自身の新しい幾何学に関する論文を、父の本の付録として付けて、高名な数学者であるガウスに送った。
すると、実はガウスも、同じく平行線問題について研究し、同じような幾何学を思いついていた事を打ち明け、「あなたを褒めるのなら、それは自分を褒めることになるから、褒めないでおこう」という、奇妙だが、確かに賛辞の言葉を返した。
「ガウス」数学の王の生涯と逸話。天才は天才であるべきなのか
しかし、ボーヤイは、大数学者は、自分の素晴らしい功績を奪おうとしているのではないか、という疑いにかられ、それで心が乱れてしまったのか、その後は、非ユークリッド幾何に関して、特に新しい知見を得る事もできず、そのうちに死んだ。
一方で、ロパチェフスキーは、ボーヤイが、その論文を読んで、自分よりも進んでいると、焦った相手だった。
しかしロバチェフスキーもまた、ガウスに見出され、科学アカデミーの通信会員に推薦されたが、その新しい非ユークリッド幾何自体は、一般にまったく受け入れられる事なく、無念のうちに世を去る。
ボーヤイとロバチェフスキー、それにガウスが考えたのは、後には『双極幾何学（Bipolar geometry）』、あるいは『ボーヤイ・ロバチェフスキー幾何学』と呼ばれる、非ユークリッド幾何であった。
平行線はいくつもあるか。存在しないか
非ユークリッド幾何学とは、第五公準を、異なる公準に置き換えた場合に成立するような幾何学として考えだされた。
言いかえれば、その新たな第五公準を採用した幾何世界は、旧第五公準が成り立たないような世界。
旧第五公準を消し去るための新第五公準は、明らかに二つある。
（a）与えられた直線Lの、上にない、与えられた点Pを通り、Lと交わらない直線が、いくつも引ける。
（b）与えられた直線Lの、上にない、与えられた点Pを通り、Lと交わらない直線は存在しない。
双極幾何は、（a）の方を第五公準の代わりに採用した時に成り立つ幾何学である。
一方で、後にはリーマンが、（b）を公準として採用した、『球体幾何学（Sphere geometry）』を構築した。
マイナスの曲率の空間。プラスの曲率の空間
直線と平行線というものについて、もう少しわかりやすくする。
直線は、「ある空間において、ある2点を結ぶ最も短い線」
平行線は、「ある空間において、可能な限りいくら延長しようとも、決して、どこかで交差することのない複数の直線」とも定義出来る。
上記ふたつの定義は、個人的には、最も最初にそう教えられるべきではないか、といえるくらいに理解しやすい。
非ユークリッド幾何学とは要するに、その表面が平面ではない空間の幾何学である。
つまり曲がった空間の幾何学なのだ。
そして曲率がマイナス（負）の場合を双極幾何学。
曲率がプラス（正）の場合を球体幾何学、と言うわけである。
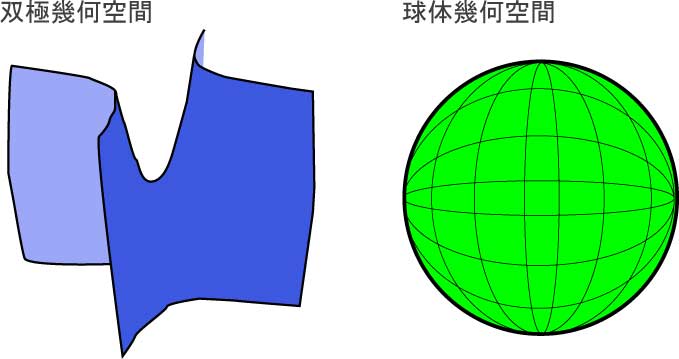
計算するまでもなく、明らかに平行線は、双極幾何学的空間ではいくつもあり、球体幾何学的空間では存在していない。
なぜ双極幾何学が先に作られたのか
非ユークリッド幾何学に最初にたどり着いた者が、3人いたにも関わらず、その誰もが、球体幾何学でなく、双極幾何学に行き着いたのはなぜか。
よく言われる解釈としては、つまり現実にありえそうなのが、双極幾何だったというわけである。
ユークリッド幾何の世界においては、「三角形の内角の和は180°」という事が証明できる。
一方で、双曲幾何的な世界では、「三角形の内角の和は180°を超えない」。
というような、ユークリッド幾何世界との相違点はあっても、公準の段階においては、両世界はほとんど共通している。
第五公準は特別か
例えばユークリッド幾何において、直線は延長出来る、とされる。
これを言い換えれば、直線というのは延長し続けたなら、無限に伸びていくもの。
そしてその事は双極幾何世界においても共通である。
だが、球体幾何世界では、直線は全て延長出来ない限界を持つ。
球体上をぐるっと一周したら、そこからもう延長は出来なくなる。
要は、第五公準は特別扱いされていたのである。
別の新たな公準と置き換えていいような、例外的なものと考えられていたわけである。
だから、第五公準以外も置き換わってしまうような球体幾何学は、リーマンが述べたとされてるように、「第五公準は別に特別なものではない」という思想を、まず持つ必要があったのだ。
驚くべき原論。エウクレイデスという人の凄さ
原論には、「これは宇宙の幾何的構造を扱っている」などとは、どこにも書かれてない。
それどころか、どうも原論に書かれた、公準や公理とは、要請という意味合いだったようである。
つまり原論は、「世界はこういうふうになっている」というものでなく、「このような条件が真なら、このような世界であろう」というものを述べた書物だった可能性が高い。
まさに文字通り、ユークリッド幾何学の本だったわけである。
もしそうだとするなら、エウクレイデスは、19世紀くらいまでの偉大とされる科学者達よりも、科学的思想において先を行っていたとも言えよう。
その時代までは、例えばニュートンのような人にとってすら、非ユークリッド幾何学は、少なくとも現実の世界がそんなのでない事は確実だから、実用的に考える事自体ありえないものだったのだ。
「ニュートン」世界システム、物理法則の数学的分析。神の秘密を知るための錬金術
だが、今では、むしろ常識なくらいに、この現実世界は、曲がった空間だと考えられている。
「特殊相対性理論と一般相対性理論」違いあう感覚で成り立つ宇宙
ちなみに、少なくとも原論は、ユークリッド幾何学の素晴らしく完全な書とは、現在では言えない。
暗黙の了解が多すぎるのだ。
例えば公準1は、ある点から点にひける直線は必ずひとつのみ、と決めておくべきである。
エウクレイデスは、ある点から点を結ぶ直線が複数ある場合のある球体幾何学を知らなかったろうから、仕方がないだろうが。
球体幾何における、そのような点と点は、つまり地球の北極点と南極点のような、点と点である。
