最も偉大な科学者で、オカルト趣味で、神の秘密の探求者
アイザック・ニュートン(Isaac Newton。1642~1727)。人類の科学の歴史において、最も重要な人物の一人であろう。
まず、影響力がすごい。
現代の人類の科学分野は、そのほとんど全て、数学的な基盤がある。そしてニュートンは、世界の様々な構造を解析するためのツールとしての数学の方法を発明した。彼の方法の応用力は凄まじいもので、彼の研究成果の恩恵を受けていない分野を探す方が難しいほどと思う。
さらには、その方法で、世界のある動作を、どのように計算し、考察するのか。物理世界の彼の数学的研究そのものが、1つのよき実例である。彼が定義した、この宇宙のあちこちでかなり普遍的と思われる物質の力の法則は、産業革命以降の様々な機械の発明や、宇宙空間を利用したテクノロジーなどにも、強い影響を与えてきた。
今は、ニュートンは、かなりオカルト趣味だったとも言われる。例えば彼は、非常に熱心に錬金術の本を読みあさっていたという。
ただし、彼のそのような傾向については長く無視されてきた。オカルトの研究記録など、科学の偉人にはふさわしくない悪い趣味かのように考える人が多かったから。
また、ニュートンは信仰心あつい神学者でもあったようだ。
プリンキピア出版までの、アイザック・ニュートンの生涯
農業の才能はなかった子
1642年12月25日(クリスマスの日)に、アイザック・ニュートンは生まれた。彼は未熟児であり、あまり長くは生きれないだろうとも言われたとか。
アイザック(ニュートン)が生まれる数ヵ月前に、彼の父は亡くなり、2年後に再婚した母は隣村へと引っ越して、幼い彼はウールスソープで、祖母により育てられた。
ウールスソープは、イングランド中東部、リンカンシャー州の集落。
それから再婚相手もまた亡くなって、母が3人の子たちとウールスソープに戻ってきたのは、アイザックが14歳の時の事。
母は、息子を学校から呼び戻し、農業をやらせようとしたが、彼は野良仕事にはあまり興味を持たなかった。
ニュートンは手先が器用で、下の子たちのため、人形の家や、
玩具の風車や、水時計を作ってあげたという。そして、暇な時間はたいてい、本を読む事で潰した。
母も、息子には農業の才はないと、早くに見切りをつけ、結局、彼は学校に戻る事になる。
母が、子の道を無理やり決めなかったのは、後の全ての数学者、物理学者、化学者、むしろアマチュアも含め、科学に魅せられた全ての人たちにとって、大きな幸運だったろうか……
驚異の年(アヌス・ミラビリス)
1661年。18歳のニュートンは、ケンブリッジ大学のトリニティ・カレッジに入学。
そして1665年6月。恐ろしい伝染病(ペスト)の流行により、ケンブリッジ大学は封鎖され、学士号を得たばかりのニュートンも、一時、故郷ウールスソープに帰省。そこで彼は18ヶ月間もの休暇の日々を過ごす事になる。
それは、人類史、科学史において、最も重要な休暇となったと語られることもある。多くの歴史家は、このわずか18ヶ月間の事を、「驚異の年」と呼ぶようになる。
光についての”決定的実験(crucial experiment)”、”微積分法(differentialandintegral)”、”万有引力の定理(law of universal gravitation)”。それらニュートンの3大業績と称されるものは、全て驚異の年の成果とされている
白い光の正体。プリズムの決定的実験
色として表現するなら白い太陽光線を、プリズムに通すと、そこに様々な色が授与される事は、ニュートンが生まれる前から知られていた事実である。
彼の時代においても、古代とあまり変わらぬほど威厳のあったアリストテレス(紀元前384~紀元前322)は、本来の光は白くて、それが弱まると他の色が生じると考えた。つまりプリズムを通すことで光は弱まり、そのために色を帯びると。
1666年の始め頃に、ニュートンはガラスのプリズムを入手。それに太陽光線を通し、壁に映される鮮やかな人工虹を楽しんだ。
しかしその内に、ニュートンは、壁に映った光は色ごとに、幅が異なっている事に、違和感を感じ始めた。
そして、いろいろ試した後、ニュートンは、プリズムから出てきた青い光だけを第二のプリズムに当てるという実験を行った。それが、後にニュートン自身が、決定的実験と名付けたという世紀の実験。
実験の結果は、ニュートンが推測していた通りになった。
第二のプリズムは、青い光を通し、青い光のみを放出したのである。それからニュートンは逆に、色付きの光を混ぜて、白い光を作る事にも成功した。
まさしく決定的であった。太陽光のような白い光は、様々な色が混ざったものであり、プリズムなどは、個々の光を屈折させ、分散させていたのだ。
白い光が弱まって色が付いていたのではなく、たくさんの色が混ざって白になっていた訳である。
『光学』
リンゴと月のエピソード
あまりにも有名なリンゴの話は作り物だと言われるが、実際のところ、嘘か本当かわからない話であり、ある程度真実が含まれている可能性もある。
ウールスソープの自宅の庭の木から、リンゴが落ちてきたのを見た時、ニュートンの目にはリンゴばかりでなく、遥か頭上の月も見えていた。
リンゴに限らず、支えてないと物は落ちてくるものだ。ではあの月はなぜ落ちてこないか?
とりあえずあれは天使が放つ光などではなく、物であると考えられる。それはすでに、偉大なる先人のガリレオ(GalileoGalilei。1564~1642)が、望遠鏡によって直に確認していた事実。ニュートンはもちろん、その発見を知っていた(ガリレオの著書『天文対話(Dialogue of the Two Chief World Systems)』は、ニュートンの愛読書のひとつだったという)。
で、なぜ月は落ちてこないのか?
違う、と、彼は閃いた。
そう、まさしく月は落ちているのだ。
月は地球に落ちてきているが、しかし横方向へ動いている速度が拮抗し、結果的に地球の周囲を回っているのだ。そもそもそうでないと、横に動く月は、地球からどんどん離れていくはずであろう。
そう考えると、月だけでない。太陽を回る惑星。惑星を回る他の衛星。これらの動きは全て説明できるのではないだろうか。リンゴが木から落ちるのと同じ原理で。
ニュートンはそう考えた。
そうして、今、万有引力と呼ばれているものが発見されたのだという。
微積分法は誰が見つけたか
地球とリンゴの距離、それと地球と月までの距離が、地球がそれらを引き付ける力と、どのように関係しているのか。
地球へ落下してくる物の速度は刻一刻と加速(少なくとも変化)する。問題は、異なる速度で動く、速度の変化する物体を比べる場合、それぞれどの瞬間の速度を基準にすればよいのかが、(当時の物理数学のいかなる方法でも)かなりわかりにくいという事。
当時は存在しなかった、ある瞬間の速度を計る普遍的な法則が必要だった。
瞬間ごとに速度を変化させる物の動きを、グラフにすると曲線になる。実質的に、ある瞬間の速度を計るのは、ある瞬間の曲線グラフの変化率を計るに等しい。
曲線の変化率の問題に関しては、ケンブリッジのニュートンの師であるアイザック・バロー(Isaac Barrow。1630~1677)も取り組んでいたが、ニュートンは、それをより実用的に発展させた。(物理学、数学に関するニュートンの研究には、バローの影響が色濃く見られが、神学に関しても、バローの影響は強かったかもしれない。バローはニュートンに、自らの後任を任せた後は、数学でなく、神の研究に生涯を捧げたという)
そうして、”微分法(differentiation)”は発明された。それは、ある対象の瞬間瞬間のデータを数学的に切り取る方法とも言える。
さらにニュートン、バローらは、それが積分という方法の逆である事にも気づき、現在の微積分法は生まれた。
 「微積分とはどのような方法か?」瞬間を切り取る
「微積分とはどのような方法か?」瞬間を切り取る
ただし(いずれにしろ、基礎的な考え方は同じであるが)、一般的に現代の微積分においては、ニュートンらと同時期、独自に同じ方法を発見した、ライプニッツ(Gottfried Wilhelm Leibniz。1646~1716)の考案した記号や表記法が使われている。
万有引力の定理
とにかく微分法を用いて、地球への様々な物体の落下速度を比べる事で、ニュートンは万有引力の定理を発見した(その理論を世間に発表する最初の場となった本には、様々な現象に関して微分を用いた計算があるが、彼はきっと、次々と、はっきりとした数量的な答が出てくることが、楽しかったに違いない)。
2つの物体の間には引力が存在し、その強さは、物体同士の質量の積が大きいほど強くなるが、物体間の距離が離れるほどに、その距離の二乗分、弱くなっていく。
つまり質量Mの物体と質量mの物体間の距離がrとすると、引力の強さFは、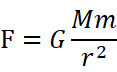
となる。
Gは万有引力定数と呼ばれる比例定数である。
秘密にされた世紀の発見
ニュートンが、その業績を認められ、ケンブリッジに席を置く事になった時、その認められた業績とは数学に関するものだった。
光学に関する発見や、万有引力の定理が、特に評価されなかった訳ではない。当初、ニュートンはその2つの大発見に関して誰にも言わなかった。数学に関しても、微積分法のことは、彼は長く秘密にした。
発見を隠した理由はいろいろ推測されているが、ニュートンは討論を好むタイプではなかった事が第一とされている。
革新的な仮説というのは、必ず多くの批判を生む。
ニュートンの前任者のように言われるガリレオや、生まれ変わりのように言われるアインシュタインとは違う。おそらく内気なニュートンは、無知な大衆の罵声を恐れた。
ただし、光学に関しては、学生への講義などで話題にされる事もあったという。
結局のところ、彼は単に、研究者として完璧主義者だったというだけの話なのかもしれない。
ニュートン式望遠鏡
驚異の年を越えて、ニュートンは優れた数学者として、名を広め始めた。そんな彼の知名度をさらに巨大にした第二の業績は、望遠鏡であった。
もちろん望遠鏡とは、対象からの光をレンズなどで一点集中させる事で、その投影像を大きくする道具。
ガリレオの時代に使われていた望遠鏡は、屈折レンズを使っていたが、ニュートンは、それでは全ての光を上手い具合に集中させられないと理解していた。
そこで、ニュートンは、鏡を使い、光を集中させるグレゴリー式望遠鏡を改良し、独自のものを開発(現在は、複数の屈折レンズを使い、効率よく光を集中させる技術がある)。
 「カメラの仕組み」歴史。進化。種類。初心者の為の基礎知識
「カメラの仕組み」歴史。進化。種類。初心者の為の基礎知識
当時の望遠鏡の中で、ニュートン式が特に優れていたのは、そのサイズであったという。ニュートン式望遠鏡は性能がかなり高いのはもちろん、小さく、非常に扱いやすかったのである。
そして、ニュートン式望遠鏡はその性能と手軽さがヨーロッパ中で人気となり、名声を高めたニュートンは、1672年1月11日に、イギリスが誇る科学学会、王立協会(Royal Society)の会員になった。
翌月、1672年2月の事だ。ニュートンがついに、光学に関する自身の発見を公表したのは。
すでに驚異の年から7年ほど。万有引力の定理と、それを発見するために使われた微積分という方法は、まだ秘密にされていた。
そして、光学に関するニュートンの発見は、彼の恐れを現実にした。
もともと、当時、光が波であるか、粒子であるか、という議論があったのだが、ニュートンの発見は、この議論に対して、まさしく火に油だった。
王立協会内で、議論は加熱し、そこに渦巻く憎しみにニュートンは心底呆れたという。
ニュートンとライプニッツ
ニュートンは、世界をよくしようとかいった意識は低かったろうし、無益な討論は好んでなかったかもしれない。
しかし一方で、プライドが高かったのか、それとも信者がうるさかったのか、1971年に公表した微積分法に関して、より早くに発表していたライプニッツ(1646~1716)より、「自分は先に発見していた」と主張。
ふたりはそれから、なんと25年もの期間、微積分法の発見の栄誉を巡り、法廷で争う事になった。
先に書いたように、現在、微積分に使われる記号などは、基本的にライプニッツ考案のものである。
ニュートンのものは、普通にわかりにくいとも言われるが、もしかしたら、彼の微積分法が、彼自身のためのもの以外でなかったからかもしれない。
エドモント・ハレーとプリンキピアの出版
エドモント・ハレー(Edmond Halley。1656~1742)はニュートンより14歳年下の天文学者。彼は、半分ヒキコモリみたいなニュートンとは対照的に、明るく、社交的な人物だった。
そんな彼は、気難しいニュートンが、生涯で最も信頼を向けた友人の一人だったらしい。
ニュートン以前にも、(定理として一般化する事こそ出来なかったが)万有引力のようなものを考える者はいた。ただし(それが真実だとして)リンゴをヒントにしたとされるのはニュートンだけである。
大半の者は、彗星からインスピレーションを受けていたようだが、ハレーもそのひとりだった。
1684年8月、ハレーはケンブリッジのニュートンを訪ねた。
星の軌道というものが、基本的に曲線を描く事を考えれば、ハレーがニュートンを頼るのは当然の流れと言えよう。微積分を考えだしたニュートンこそ、まさしく曲線のエキスパート中のエキスパートだったのだから。
しかし、ふたりの間にどのようなやりとりがあったのかは謎が多い。ただひとつ言える事は、ニュートンが、ハレーの説得に折れたという事。
公表のタイミングとしても、まさしくベストだった。
ハレーを始め、証明こそ出来なくとも万有引力に気づき始めた人たちがいる。このままでは微積分の二の舞になる可能性もあった。
さらにニュートンは、万有引力の定理を隠してはいたが、腐らせていた訳では決してない。彼はハレーが訪ねて来た時、すでに発見されていた太陽系を巡る惑星の軌道まで完全に計算を終えて、推論は完璧に確信となっていた。
そういう訳で、ニュートンは、1686年、全3編の科学書『プリンキピア(自然哲学の数学的諸原理。Philosophiæ Naturalis Principia Mathematica)』を書いて、出版した。
『プリンシピア 自然哲学の数学的原理 第1編 物体の運動』
『プリンシピア 自然哲学の数学的原理 第2編 抵抗を及ぼす媒質内での物体の運動』
『プリンシピア 自然哲学の数学的原理 第3編 世界体系』
この本は、それまでのニュートンの物理世界の数学的研究の集大成のような内容で、基本的な力学、振り子や空気抵抗、流体や振動の伝搬から、万有引力と、その世界定理を背景とした星々の動きの具体的な例と、かなり多岐にわたっている。
そしてこの本に関して、出版費用、印刷所との契約、校正などのチェック作業といった、内容以外の全ては、ハレーが担当したらしい。彼はそれだけ、そこに書かれた理論、世界観の正しさをはなから確信していた。ニュートンがどのような人かをよく知っていたのである。
プリンキピア。物理世界の力学系、宇宙の哲学的考察のための幾何学
プリンキピアの1と2巻は、物理現象の数学的な定義や証明が、ひたすら続く。構成的には完全に、エウクレイデスの『原論』を参考にしていると思われる。最初に出発点となるいくつかの公理が示された後、すでに明らかとなった情報ばかりを用いて、次々新しい話に移っていく。
3巻では、物理現象の様々な数学的定義を、実際の世界の動作に当てはめ、様々な数値を算出している。
最初の世界の理論
プリンキピアという本は、出版当時からかなり売れたらしい。ただ当時、その数学的考察ばかりの内容を真に理解できる者は少なかったとされる。
しかしこの本に、何か凄いことが書かれている事は、一般大衆にもわかったろう。ハレーを始め、その内容を理解できた、高名な科学者たちは、誰もが、ニュートンの研究の成果を大絶賛したそうだから。
それに万有引力の定理は、統一理論、つまり世界というものを説明できる最初の理論でもあった。
なぜ海は高低を変えるのか。なぜ星は球体なのか。なぜ星は星の周りを回るのか。なぜリンゴは木から落ちるのか。
万有引力の定理は、全てを説明したのである。
それはまさに、知性の勝利とも言えた。
力学と幾何学の関連付け
序文で、ニュートンは、古代の力学の考え方と、より洗練された方法に関して書いているようである。
〔古代、パップス(Pappus。※4世紀頃のエジプトの数学者)が書いた「力学(Mechanicam)」は、自然現象の真の研究において最も多くのことを行ったが、近代の研究者たちは、実質的形態や隠れた性質は置き去りで、自然現象を数学法則に基づいて説明しようと努めた……
機械職人は実用性を重視し、あまり正確には作業しないことが多い。結果的に彼らは、すべての力学を幾何学と区別する。正確なものがすべて幾何学、それほど正確でない(もちろん全くのごちゃごちゃでなく、ある程度は正確な)ものが力学と呼ばれる。
しかし間違っているのは芸術でなく、芸術家だ。あまり正確に作業できない人は、不完全な機械工。もしある人に、最高精度の作業が可能だとしたら、その人はすべての中で最も完璧な機械工となるだろう。
幾何学の基礎となる直線と円の記述は、力学の範囲にある……
幾何学は、力学の問題の解決方法を与えられる……したがって、幾何学は、実践的な力学の基礎にもなる。正確な計測方法を提案できる……
一般に幾何学においては大きさ、力学においては動きにより限定的であることが起こる。では、どのように、論理的力学(Mechanicarationalis)、あらゆる力から生じる運動の科学を考えるか。あらゆる動きに必要な力の結果があるが、それは正確に実証されたりする。力学のそのような部分として、古代の人は「五つの力(Potentiis quinque)」を定義した。彼らは、(手動によらない)重力を、重りの移動と同じように考えていた。
……しかし、手動の力でなく自然力について書く場合、私たちは主に重力(Gravitatem)、軽さ(levitatem)、弾性力(vim Elasticam)、流体の抵抗(resistentiam Fluidorum & ejusmodi)、および引力か推進力に関係するものを扱う。そして私たちはそれらを哲学の数学的原理として提案する。というのは、哲学のすべての難題は、運動現象を手がかりに自然の力を研究し、その後、それらの力から残りの現象を実証するということに集中しているように思われるから……〕
ニュートンは簡単に、線や円を基礎としているのが幾何学というようにも書いているが、実際には、それは動作しているあるものの力学系を考察するのに利用できる。ところが、実際の我々が直面する力学系というものは、それを動作させる(曰く不完全な)我々が与えてしまう余計な(あるいは実用的に問題のない範囲で許される、例えば利用者にとってはどうでもいい)誤差のために、正確なものである幾何学とは異なる印象をもたらしてしまう。
結果として、様々な部分がかなり完璧に正確であるものが幾何学で、ある程度は正確であるが完全に正確とは言えないものが力学というように、(少なくとも実用的には)区別されてしまったり。
しかしニュートンは、幾何学と力学は別々のものであるが、関連付けて考えることができるとする。
1つ重要なことは、幾何学も力学系も、考察にあたって完全に自由であるわけではないこと(むしろ、ある定義の与えられた系において、まったく完全に自由というようなものがあるだろうか? あるとして、それは世界そのものとかだろう。世界の部分を考える時は、はなから部分という制限が存在しているから)。ニュートンは、幾何学は大きさ、力学は動きのために限定的なものであると考えた。
これは、ニュートン自身が開発(あるいは実用的に改良)し、実際にいろいろ応用した、微積分という方法のことを思えば、結構興味深いのでなかろうか。
ニュートンの微積分法は、基本的には(途切れない限り、いくらでもぐにゃぐにゃ曲がることのできる線という意味での)曲線の部分的考察と言える。つまり、線として定義できるもの(例えばある物質が動く道筋)の、ある(刻一刻と動作を続ける物質に関しては、ある瞬間の空間的位置とも言える)部分の接線(隣接する円と、ただ一点でのみ接している直線)を描く(あるいは定義する)。物理的な物事の解析に利用する場合は、さらに(導出された数式の)その意味を考察する。
このような方法は、まさに、幾何学的な、力学系解析の方法と言えよう。そして、この方法がどれほど実用的で、どれほど応用性に優れたものであるかは、今は多くの人が、ニュートンよりもよく知っていると思う。
(現代では、普通は微分の操作には、ある幾何学的図形と等価な代数式を使うが、ニュートンの時代には、それは邪道と認識されていたようである。少なくともニュートンは、可能な限り直接的な図形を利用し、数式は避けているような印象)
また、以下の疑問は注目すべきかもしれない。
〔1、2巻の命題により、数学的に証明された天体現象から、物体が太陽や惑星に個別に向かう場合の重力が導き出せる。さらに、それらの力から、惑星、彗星、月、海の運動までも、推定が可能だ。
同じような推論によって、他の自然現象も機械的な原理から導き出すことができたらいいが。というのは、私は実は、すべてのことが、ある力に依存しているのではないかと少し疑っているのだ。その力によって、物体の粒子は、まだ知られていない原因により、互いに打ちあったり、規則的な形に連帯したり、離れたりする。哲学者たちはこれまで、この未知の力のために、自然の探求において失敗ばかりだったと〕
これは、万有引力が全てを説明するかもしれないというものではなく、もっと根本的に、全ての世界の動作に関連している、何らかの隠された力があるのでないか、という疑問だろうか。
現代的に言うと、これはこの世界の統一理論の可能性についての言及と言えるかもしれない。
ニュートンは、世界の第一原因としての神の可能性を強く支持していた節があるが、上記の文脈的には、そこでいう全てが依存する未知の力というのは、第一原因(つまり神)というわけでもないと思う。
プリンキピアにおいてもそうだが、ニュートンは時々、明らかに、この世界の物理的システムと、この世界のクリエイターである神の意識的なこの世界への影響を区別している。
ようするに、この世界の全てに関連している基礎的な力があるのだとして、その力そのものが神様という訳ではない。それは、神様がこの世界に設定した基礎要素と考えていたようなのだ。
また別のところでニュートンは、実際にこの世界を創った神は、この世界の理から外れているような存在であって、この世界の住民である自分たちには、その神様という存在そのものを直接的に理解する術がないかもしれないと推測してもいる。一方で、この世界の様々なシステムは、数学のようなツール(知的道具)をうまく使えば、色々理解できるかもしれないという希望を抱いているような印象がある。
もしかしたら彼は、世界を理解しようとする試みにおいて、人間が目指せる限界点を推測していた(そのつもりだった)のかもしれない。それが、この世界の全ての要素と関連している基礎的な力でないかと。
世界をどう定義していくか
最初にいくつかの物理量が定義される。
〔定義1=物質の量は、その密度と大きさの組み合わせから生じる量である。
例えば空気は、2倍の空間では2倍の密度になり、物質量は4倍。圧縮や溶融により凝縮した雪や粉塵などついても同様に理解できる。
物質の量に関して、様々な原因で異なる方法で凝縮されるすべての物質に対して同じ比率が成立する。ただし、部分の間の隙間を自由に通過するような性質は考慮しない……
定義2=運動の量は、物質の速度と量を組み合わせたものから生じる量。全体の運動は、個々の部分の運動の合計。2倍の体の2倍の速度は4倍の速度に相当する。
定義3=物質の力とは生来の抵抗力であり、それによってあらゆる物体は、それ自体であるかぎり、静止状態または直線方向に均一に移動している状態を維持する。
この力は常にその物体に比例し、概念的な方法を考慮しないなら、慣性質量と同じとも言える。物質の慣性によって、あらゆる物体がその静止状態または運動状態から難しく乱されることがある。したがって、この固有の力は、非常に意味深い「慣性力」と理解されることもある。
この力を発揮するのは、加えられた別の力による状態の変化がある場合だけ。さまざまな観点からのその運動と抵抗の力として現れる……〕
このような定義は、おそらく、適当にいくらでも決めることが可能ではある。しかし決して詐欺的なものではない(詐欺的なものにもできるだろうけど)。うまくやれば、これは実用的な方法でもある(少なくとも、古代ギリシャから伝えられてきた、人の、伝統的な論理の方法)。
世界は本当に、(例えば、古代にピタゴラスが考えたとされるように)数学的に考えられるシステムによって支配されていたか? ニュートンはかなり懐疑的だった印象がある。そもそも彼は多分、本当の(この世界を創った)神の目的、その世界を作った謎の力(原理)とかに関して、人間(この世界内の知性)には決して真に理解できるようなものではないだろう、と推測していた。
ただ、世界の真の原理、神の真のシステムがどのようなものであるかというのは、ある物理系(ある範囲、ある部分、ある世界など)を数学的に考察する上で、それほど重要ではないのだ。まさに実用的に考えるならば、重要なことは、定義された様々な法則群(例えば「物質の量は、その密度と大きさの組み合わせから生じる量」など)が、全て矛盾しないで機能すること。
ニュートンの時代の人たちより、我々の方がその理屈は納得しやすいと思う。デジタル機械技術で実現されている様々なバーチャル再現物、体験などはどうか。コンピューターのスクリーン(モニター)に投影されたデジタル絵や、五感を騙すことで実現するバーチャル体験、あれらこそまさしく、ある物理系の各要素に数値を当てはめてコントロールすることで実現している、実用的偽物と言えるだろう。
そして微積分のような数学の方法を利用したシミュレーションが、世界のある動作に当てはまるなら、実際それがどのように機能しているにせよ、実際的にはその数学的計算によって、次の動作や以前の動作を予測できるのと同じだ。だからこそ、ニュートンの万有引力の法則により、ある星の未来の位置を測定できたりするわけだ。その実用性は、万有引力の定理が本質的に正しいかどうかは関係ない。
例えば、実際は質量が引力を発生させるようなことはなく、ただ神が、宇宙という有限空間を置いた高次元空間に、宇宙内の物質の重みによるへこみが生じ、結果、高次元空間でへこみに転がる物質の動きが、宇宙内部の人間の感覚では、物質同士の間に引力を発生させてるように見えるだけなのかもしれない(ニュートンよりずっと後のアインシュタインによると、万有引力という秘密の力より、そのような世界観の方が正しい可能性が高い)。
 「特殊相対性理論と一般相対性理論」違いあう感覚で成り立つ宇宙
「特殊相対性理論と一般相対性理論」違いあう感覚で成り立つ宇宙
〔定義5=向心力(Viscentripeta)とは、中心に向かうか、または押されるかのように物体がある点に向かって引き寄せられる力のこと。例えば重力(gravitas)には、物体を地球の中心に向かわせる傾向があり、磁力(Vismagnetica)は、鉄を磁石の中心に向かわせる。向心力は、惑星の直線運動を、強制的に曲線の回転にする……
定義6=向心力の絶対量は、中心から周囲の領域に伝播する原因の効率に応じた、その大きいか小さいかの測定値。ある磁石ではより大きな磁力、別の磁石ではより小さな磁力を発するというような。
定義7=向心力の加速度は、所定の時間内に発生する速度に比例する測定値。同じように、磁石の力は、距離が小さいほど強く、距離が大きくなると弱まる。重力も同じようなもので、(振り子の実験が証明しているように)最も高い山の頂上より、谷の方が強い。(後述するように)地球から遠く離れた場所では、重力はさらに弱くなる……]
ニュートンは当然のように、磁力というものが重力と同じように、その強さが距離に比例して変化すると書いている。
(構造的に万有引力と似ているから)、おそらくニュートンの数学体系に影響を受けていたとされる、荷電粒子間の引力(電気的な引力、または斥力)に関するクーロンの法則には、同じような磁気力版がある。しかしこれは普通、ニュートンが生きていた頃より後の発見とされている。
ニュートンは、磁力というものをどのように考えていたか。それもわりと謎だが、いずれにしろ、そのような、重力とか磁力といった、自然界の力が、本質的に存在していようがいまいが、あまり関係なかったろう。少なくとも彼が、プリンキピアという本で試みようとしていた知的研究においては。
 「電磁気学」最初の場の理論。電気と磁気の関係
「電磁気学」最初の場の理論。電気と磁気の関係
〔私はもはや力の原因とか、物理的な座は数えていない。速度が運動に相当するのと同様に、加速力は動力に相当する。なぜなら、運動量は物質量に含まれる速度から生じ、駆動力は同じ材の物質量に含まれる加速力から生じるから。物の個々の部分に対する加速力の作用の合計が、全体の原動力となるのだ。
したがって、重力加速度、またはかかる重力がすべての物体で同じである地球の表面近くにおいては、重力は実質的に物体の重量である。重力加速度が小さくなる地域に移動すると、物体の重量も同様に減少する……
引力、推進力、傾向などが中心に向かう場合、これらの用語を相互に交換可能に使用し、物理的ではなく数学的な意味でのみこれらのことを考慮する。したがって、読者はこれらの用語を私が使用した時、行動様式、作用、または物理的な原因などをどこかで定義していると誤解しないよう気をつけてほしい。また、物理的中心(数学的な点)に力を与えると述べることがあっても、それは、中心を引き付けるものとか、中心の力という意味ではない。
……つまり私は、時間、空間、場所、運動を誰もが常識としてよく知っているようには定義していない。一般の人々は、これらの量を感覚的なものとして以外の理解方法では考えていないことは指摘しておきたい。そこからある種の偏見も生じてきた。それを取り除くためには、それらを絶対的と相対的、真実と見かけ、数学的と一般的に区別することが適切だろう〕
つまりニュートンは、具体的にどんな自然の力が存在してても、またはそんなもの実はなくても、数学的な物理世界考察には、それほど大きな影響がないと考えていた、と思う。なぜなら、数学的考察において、計算要素となるのは全て数学的概念として定義されたものであって、現実に対応した時のものをどう考えるかは、全く別の問題だからだ。そしてプリンキピアはあくまでも、自然の哲学そのものでなく、その数学的原理の本が主題の本である。
無限概念を利用した曲線の分析
微積分法はライプニッツも独自に発明していたし、そもそも考え方自体は、ニュートンの師(バロー)もいい線いっている。
そもそもプリンキピアを出版する頃には、すでにニュートン自身、その方法に関して完全に公表している。それでも、当時としては、まだまだ最新と言えたその方法を使った、具体的な分析の例が、この本には大量にある。
例えば、最初の区切りという感じの、補助定理11(それだけ抜き出して見ても、けっこう意味不明だろうが)
〔補助定理11。角の接点における消失する部分は、隣接する弧の二乗比において最後のもの〕
ここでの命題の証明には、無限の概念が少し利用されている(つまり微積分的。ただ問題とその証明自体は、歴史的な価値が少しあるくらいだろうけど)。注目したいのは、やはり方法論に関する解説。たいていの人にとっては、現代の一般向けの数学解説本の方が、よほどわかりやすいと思う(ちなみに、これでもわかりやすくするため、けっこう意訳しているつもり)。ただここでの、微積分という方法の捉え方は、すでにかなり現代的と言える(というより、現代的な認識を提唱した一人が、ニュートンだったのだろうか)
〔……つまり点Aの曲率は無限に小さくも無限に大きくもないと定義し……接線ADと曲線ABの間の点Aを通る円を描くことはできない。接触角は円形のものよりも無限に小さくなってしまうから……
私がこれらの補題を主張したのは、古代の幾何学者のやり方に従って、不条理な部分までの複雑な実証を導くような退屈から逃れるためである。
……物質量が粒子で構成されていると考える場合、または直線の代わりに曲線を使用する場合、分割できないではなく、分割できる一時的なもの、確定部分の合計と比率でなく、合計と比率の極限が存在する……
このような計算の際に、消滅する量の最終的な割合などはない。なぜなら、それらが消える前のものは最後でなく、それらが消えた場にはそもそも何もないから。しかし同じ議論により、物体が特定の場所に向かう時の、極限範囲における速度など存在しないという主張ができてしまう。なぜなら、物体がある場所に到達する寸前と、到達した最後の場はなく、存在しないとなるから。
答は簡単だ。
極限範囲の速度値とは、物体が動かされているその時の速度を意味しているのだ……〕
ニュートンは物体の動作を幾何学的に考えている訳で、例えば、刻一刻と速度を変化させる物体の速度の数値を、物体が進む(あるいは進んできた)軌跡を構成する各点としている。そしてここでは、ある瞬間の速度を知るために、ある点の周囲を無限に狭める場合を考察しているのだろう。それは実際、幾何学的空間において、微積分が用いられた時に起きていると思われる動作である。
絶対空間。バケツと水の実験の意味
万有引力の定理、微積分、光の色。それらの他に、物理学の本でニュートンにスポットが当てられた時によく語られるのが、”絶対空間(Absolute space)”であろう。
一般によく紹介されている、ニュートンが定義した絶対空間は、やはりプリンキピアに書かれたものである。
現代の本ではよく、ニュートンの絶対空間は、彼が、特に大した根拠もなく、基本的な世界要素だと決めたもので、そして、結局は間違っていた可能性が高い、というようによく語られている(現代では、時間と空間が強く関連付けられ、動いている物質の時間の変化、あるいは変化速度の変化のため、そもそも世界の本質的な要素として、絶対的な空間という概念を定義することが難しくなっている)
本当はどうだったのだろう? 実際のところ、絶対空間とは何なのか?
〔絶対空間と相対空間は、形も大きさも同じで、数が同じであるとは限らないものだ〕とニュートンは書いた。
さらに、〔場所とは、物体が占める空間の一部〕、そして〔全体の運動は部分運動の合計と同じで、つまり、全体のある位置からの変換(※移動)は、部分のある位置からの変換の合計と同じ〕。それらの考え方を踏まえ、ニュートンは〔絶対的運動は、絶対的な場所から絶対的な場所への物体の移動であり、相対的運動は、相対的な場所から相対的な場所への移動〕とした。
例えば、この宇宙そのものが(おそらくニュートンがそう考えていたように)絶対空間として、(これはニュートンが実際に書いている例だけど)地球が動いた時、地球に対して相対的に留まる空気の空間がある場合、地球と空気空間には相対的な位置関係がある。この場合、地球が絶対空間である宇宙の中を動いた時、宇宙のある位置aにあった地球は、別の位置bに動くが、位置aやbに固定されている宇宙のある要素と地球(や空気空間)との距離(の数値)は明らかに変化する。しかし、地球とともに動く空気空間の中の粒子αと、地球を構成している粒子の1つβの距離関係は変わらない。
つまり、地球と空気空間は、絶対空間の中では明らかに移動(絶対的運動)しているが、互いに相対的には移動(相対的運動)していないと考えられる。
別の例として、ニュートンは船と地球の動きを考察している。
地球の海で移動する船(内部の空洞を含む構造全体)に、人が(つまり船の内部に)乗っているとする。この場合、船が動いていても、人と船は互いに、相対的には停止している。
しかし、地球が静止している場合、船内で相対的に静止している物体は、船が地球上を移動する速度で絶対的に移動している。地球も動く場合は、(総体的な)物体の絶対的動きは、部分的な静止空間での地球の動きと、地球と船の相対運動が合わさったものとなる。人も船内で相対的に動く場合は、さらにそれも考慮しないといけないだろう。
〔つまり、船が回転する地球上にあるために速度10010で東に移動している時、風を受けて船が10の速度で西に、船員が1の速度で東に向かって船内を歩くとする。すると船員は10001の速度で真に絶対的に動かない空間を移動することになる。また(※船員視点では)地球が相対的に西に向かって9動いているとも言える。
また、天文学においては、絶対時間は、一般的な時差計算により相対時間と区別される。なぜなら、一般に時間の尺度として利用される自然の日数と定義されてる時間概念は、不平等(※これはまず間違いなく、日常で利用している時間が地球表面の各位置と太陽の光の角度を基準にしているからだろう。ある地域が太陽の光が当たっている朝なら、球体の地球の反対側では夜)だからである。天文学者は、より正確な時間で天体の動きを測定するため、この不平等を修正する〕
そしてニュートンは、時間の問題にも(絶対的な空間と合わせて)触れる。
〔時間を正確に測定できるような、同じ動きなどは存在しない可能性がある。あらゆる動きは加速したり減速したりできるが、時間の絶対的な流れを変えることはできない。物事の存在の継続時間、または持続性は、動きが速いか遅いか、またはまったく同じかに関係なく、明らかに同じだ……
時間の部分の順序が変更できないように、空間の部分の順序も変更できない。物体をある場所から移動させれば、それはそれ自身から移動するも同じ。なぜなら、時間と空間はそれ自体のものであり、場所としての万物そのものだからである……
それら(※時間と空間)は本質的に、それらの場所そのものであり、それらが場所を変えると考えるのは、かなりばかげている。それらは絶対的な場所であり、実質的にそれらの場所からの変換だけが絶対的な動きである。
しかし、空間のそのような(※絶対的な)部分は目に見えず、一方で私たちは感覚によって互いを区別できるため、私たちは一般にそれらの代わりの賢明な手段を使用する。なぜなら、私たちは不動であると考えるあらゆる物体からの、物の位置と距離から、場所全体を定義する。次に、我々はまた、そこから動く物体を想像する限り、前述の場所に関するすべての動きを推定する。
という訳で、私たちは場所や動きが絶対的なものとして相対的なものを使うが、日常においてはともかく、哲学においてはそれは厄介な問題だ。実際、真に静止している物体など存在しない可能性もある……
真の絶対的な運動は、静止しているとみなされるだけの物体との位置関係を基準に定義できない。絶対運動物体の外部の物体は、単に静止していると見なされるでなく、実際に静止していなければならない。そうしないと、周囲からの変換を除き、含まれるすべてのものは周囲の真の動きにも属することになり、その変換によって取り除かれると、それらは真の静止でなく、単に静止していると見なされるだけのものになるだろう。周囲は囲まれたものに関係しているから〕
ニュートンは、水を入れたバケツをワイヤーで吊して、ワイヤーをねじり上げ、手を放すというような実験をしたらしい。
もちろんバケツはくるくるまわるが、最初はバケツ内の水はほぼ静止していて、その表面は平ら。しかしバケツの回転速度が上がると、バケツの運動が徐々に水に伝わり、結果的に水も回転を開始し、表面は、真ん中がくぼんだような形になる。
それからさらに、水はバケツの中、真ん中からの圧力に押されるような流れで上昇する。
ニュートンは、ある物体というのは、その物体の表面と内部構造、そしてそこに含まれている全ての粒子の集合体と(おそらく現代でも、多くの人がそうだと考えているのと同じく)考えていた。それで、バケツの中の水は、1つの物体として考えることができるだろう。
普通、この地球上の環境において、水を構成している粒子のそれぞれの引力はそれほど強くないから、何も止めるものがなければ、それは広がりやすい。しかしバケツという個体の中にある時、そのバケツの形に、水という物体(その全空間)の場は制限されている。
バケツの回転の影響で、内部の水が回転し、その中心の方の要素量(構成要素、構成粒子)のいくらかが外側に向かう時、しかしバケツという場の制限のために、水はそのまま横に押され続けることはできない。結果的には、バケツにより止められていない上の空間へと、溢れた要素は逃れることになる。つまり、それを観察する地球の人の視点から見れば、水は上昇する。
世界に水とバケツだけがあるわけではない。ニュートンは、このバケツ実験を行った時、おそらく回転(一般的には加速運動)する水が、何に対して回転しているのかを知りたがっていた。
それはつまり、運動という現象の、おそらく理解されていない本質についての問いだった。
素直に考えるなら、バケツが回転を始めたその瞬間には、水は平らだったろう。そしてこの水を静止しているとみなすなら、回転するバケツの相対的な違い(互いの回転量、つまり加速度の差)は、おそらく水が動き出してからよりも大きい。むしろ水の上昇運動のピークは、バケツに対する相対的な加速度が最も小さい時(あるいは、純粋に数学的な空間で考えるならば、それがあるマイナスの数値になった時)と言えるだろう。
つまり、このバケツ実験の水の動きは、バケツと水の相対運動で説明することが、多分できない(厳密には、動きの量が小さいと動きの量が増えるという、感覚的に奇妙なことになりうる)訳である。
〔つまり、回転を引き起こした力は周囲の物体との水の移動に依存していない。真の円運動はそのような移動を通じて定義されない〕というのが、ニュートンがバケツ実験から得た結論の1つであった。
ここで、真の円運動というのは、ほぼ間違いなく、絶対空間に対する物体の動きであろう。
もしかしたらニュートンの絶対空間は、数学的な計算のために定義したものというより、世界そのものの考察の途中で導出されたものだったのかもしれない。発想的には、この世界に必要と思われる第一原因(神)と似たようなものとも言えるだろうか。
また、そもそも水は、バケツでなく、バケツの外部(または外部の何か)との相対的運動を起こしているのでないか、という、当然すぐに出そうな疑問も、もちろんニュートンは承知していたと思う。
〔しかし相対運動は、外部とのさまざまな関係において無数にある。関係自体と同様に、それらは、単一運動に参加する限りは、真理の影響をまったく受けていないだろう。
したがって、固定されているような惑星などの天体も、その静止状態は相対的なもので、実際は動いている。なぜなら、それらは(本当に完全停止している場合と異なり)互いに対する位置を少しずつ変えているから……
つまり相対的量とは、実質的には、そもそも量ではなく、一般的な人が、測定の基準に使う、いわば感覚的測定値で、偽のものだ。
しかし現実において言葉の意味を定義する場合、時間、空間、位置、運動などの言葉は正確に理解されるべきであり、ここに測定量が暗示されているなどと仮定することは異常事態で、愚かなことだろう〕
ニュートンが、天体の動きに注目した理由は、間違いの元となりそうな、複雑に絡み合う様々な要素が、なるべく一番存在していなそうな場が宇宙空間だったからではなかろうか。地球上でのバケツ実験では(バケツという個体に隔てられた)地球表面の物質群とバケツ内の水が相対運動をしているというように考えることは容易い。だが、何もない宇宙空間というところに置かれ、(そこに本当に他に何もないのだとすれば)そこで動く(相対的位置を変化させる)天体群は、いったい何と相対的に動いているのか。
むしろ宇宙空間でバケツ実験を考えれば、ニュートンの疑問はよりわかりやすい(実際、ニュートンはそのような思考実験を行ったようだが、もちろんそれは思考実験でしかないとも言える)。他には相対的に動くものがない宇宙空間で、バケツ(水が中に入ってるなら、中の水も)は何に対して回転しているか。
(それが例えば、この宇宙でないとしても)全ての物質の運動に関して、基準となる絶対的な座標系、絶対的な空間が存在するはずだと、ニュートンが推測したのも、おかしな話ではないだろう。
そして、こうして提案された絶対空間が本当に存在するのなら、ある物質が本当の意味で動いているというのは、絶対空間に対して動いているということで、本当の意味で静止しているというのは、絶対空間に対して静止していること。それとは異なる相対的な運動は(絶対的空間のどこからの視点で見るによって、動いているか静止してるかも、またはその速度も変わってしまうと思われるから)実質的には幻想にすぎない(つまり決して、絶対的に運動とは言えない)と考えた。
しかし結局はニュートンも〔絶対空間は、その本性として、どのような外的なものとも関係なく、つねに同じであり不変不動であるもの〕などと定義するくらいしかできなかった。
ところで、この、ただ永遠にそこに存在しているというような絶対空間は、やはり第一原因(神)のことか、あるいは第一原因と関連した直接的に関連している何かであったろうか。
残念ながら、これらが何か関連あるか、あるいは関連してるとしてどのように関連しているかについては、ニュートンもおそらく、まともに考えることなどできなかった(この考察を試みようとしなかったとは思えない。できなかったのだろう)。
彼が神について語る時、それは本質的には決して理解できるようなものではないだろう、というようによく書いていたみたいだが、そのように諦めていなかった時期もあったろうか。
エーテル、霊魂、秘密のシステム。万有引力の原因
現実の世界の動作、例えば天体の動きに関する、万有引力の考え方などを用いた、動作分析の具体的な例は、基本的に3巻の内容となる。
1、2巻のほぼ全体を通して行われているのは、数学的な定義と証明。万有引力というのは、そのような数学的考察の中で、世界の総体の動作を説明するために導入された、様々な質量が有する引力のことで
ただし、すでに1巻の最後の方で、万有引力についてのニュートンの考えが見られもする。
〔ここで物体Aの絶対引力は物体Bの絶対引力に対するものであり、Aに向かうすべての物体の加速引力は、等距離にあるすべての物体のBに向かう加速引力と関係している。したがって、物体BからAへの加速引力は、物体AからBへの加速引力にもなる……
これらすべての物体の力は、物体自体がそうであるように、相互に対して絶対的になる……
磁気のように、物体に向かう力が、その性質と量に依存するということは理にかなっているだろう。そして、この種のパターンのたびに、各粒子に適切な力を割り当て、その力の合計を導出することにより、物体の引力を推定できる。
そのような引力が実際にはどのように働いているか。物体が互いに押し合う作用によってか。それとも送り出されて互いにかき混ぜ合う霊魂によってなされるのか。あるいはそれぞれの媒体のエーテルや空気の作用によってなされるのか。あるいは肉体と非肉体が互いに浮遊しているシステム上に生じるのか。
一般的な意味では、力の種類や物理的性質としてでなく、数学的な量と比率を考慮し、私は単に力積(インパルス)という言葉を使う〕
質量、物質間に働く引力の原因として、霊魂とかエーテルとか、いろいろ非物質的なものが想定されている感じであるが、これらも、絶対的空間である宇宙の中の、相対的要素として想定されてたのだろうか。絶対的な神が存在しているかどうかはともかく、この宇宙そのものにも、物質だけでは説明できない何かがあるとか。
もしも、そのような非物質的要素さえも、数学的に(つまり数学空間において)分析できる、とニュートンが考えていたのだとしたら、それはまた興味深い話だ。現代において、そのような世界観の可能性は、つまり(まさに世界要素の数学的再現とも言える)デジタルテクノロジーというもので、再現できる対象について楽しい希望を抱かせてくれるだろう。
そしてシミュレーションというものは、実際的にはどの程度リアルの再現と言えるのか。例えば微積分法は、夜空に見える天体の動きを説明するだけでなく、いつかそこに、地球生物がいけるかもしれないという、かなり実用的な希望さえ我々に与えてくれた。もしかしたら、いつか数学の方法は我々に、魔法を与えてくれたりもするだろうか。
彗星は生命の種を運んだか
ニュートンが、プリンキピアで扱っているのは、数学的に分析した宇宙の物体の動作でしかないと、ニュートン自身が考えていた印象が強い(この世界システムの、本質的な原因に関する哲学的な考察などはほとんどないと言っていい)。
そして、3巻において、ニュートンは、実際に具体的な様々な観察記録の数を計算式に導入し、万有引力というものが生じている範囲(つまり、本が書かれた当時に知られていた、実質全ての物理世界)の現象を、いろいろ考察している。
ニュートンの万有引力が普遍的な世界観において、非常に有名な予測の1つは、ハレーによる彗星の周期であろう。
だが例によって、そのような数学を用いた予測は、彗星というものが、具体的にどのような物体(構造体)であるかということに、関係なく行える。
重要なのは、世界、あるいは世界の一部を数学空間として定義した時、そこで普遍的に機能すると思われる法則があり、さらに一般的に全ての物体に共有される概念としての質量(物質の量)も定義したら、あとはその世界の普遍的法則により、観察で確認されているある量の物体がどのように動くか計算すればいいだけ。そうしたら、普遍的法則を無効にしてしまう特殊な(あるいはまだ知られていない)作用が、どこかで生じない限り、例えば、ある彗星を構成する各要素を全然知らないでも、その彗星の未来における位置を予測することができる訳である。
ようするに、ニュートンもハレーも、いくつかの彗星の軌道をかなり正確に計算することはできた。しかし、その構成素材などの情報を知る術はほとんどなかった。
それでも3巻の最後の方。彗星に関する考察から、ニュートンが、まさに彗星のような天体の実態にも、強い関心を抱いていた印象を受ける。
まず〔……彗星の本体が惑星の本体と同様に固体で、コンパクトで、固定されており、耐久性があることは、難なく想定できるだろう。というのは、もしそれらが地球、太陽、惑星の蒸気や噴出した気体にすぎないのなら、(強い熱にさらされる)太陽の近くを通過する彗星は、即座に崩壊してしまうだろうから〕という推測について。
ニュートンの理解としては、気体というのは、液体が熱により変化したものだったようだ(つまり、今の我々の理解と基本的に同じ)。そして、ある温度で揮発性(つまり液体が気化する性質)を示した物質は、その後はもう、さらなる熱の上昇に驚くべき弱さを示す。
としたら、もしも彗星というものが、そのような気体(揮発性物質)だったならば、太陽に近づき、その熱の影響が高まった時に、崩壊せずにいれるほどの強さ(硬さ)を見せるのは、ほとんど考えられないであろう。
 「化学反応の基礎」原子とは何か、分子量は何の量か
「化学反応の基礎」原子とは何か、分子量は何の量か
またニュートンは、ある物体に熱が与えられた時、その後に熱が保存される時間に関して、条件が同じであるなら、より大きな物体の方が熱を保存している時間が長いだろうと書いている。ある物体が大きくなった時、物体全体の構造の中で、表面積(つまり、冷却の原因となる周囲の環境との接触部分)が占める割合が小さくなると計算できるから。
ただし彼自身は〔実は、熱の持続時間は、直径の増加よりも小さな割合で増加する何か潜在的な原因によるものでないかと疑っている。いつか、熱の増加の割合が正確に実験で測定された時、答も明らかになるだろう〕と書いてもいる。
 エントロピーとは何か。永久機関が不可能な理由。「熱力学三法則」
エントロピーとは何か。永久機関が不可能な理由。「熱力学三法則」
ニュートンよりもう少し後の時代(18、19世紀くらい)の生物学の本とかだと、「熱や電気こそが、生物の魂の作用と思われるものの、実際的な原因なのでなかろうか」というような説がわりと語られるようになってくる(あるいはニュートンの時代には、すでにそのような説がそこそこ一般的になっていたのかもしれない)。ニュートンも、物理数学空間において熱(ある種の物体運動)として定義できる現象は、実は全世界システム上において”真の熱現象”と言えるようなものの、部分、あるいは副作用的なものにすぎないのかもしれない、と考えたことがあったかもしれない。そうだとするなら、物体の熱の保存時間の変化率のような数値が、その真の熱現象をよりはっきり示唆する手がかりになりうる、こともあるかもと期待しても、おかしくはないだろう。
 「ラマルク。進化論と動物哲学」用不用説、生物世界唯物論、そして系統樹の発見の物語
「ラマルク。進化論と動物哲学」用不用説、生物世界唯物論、そして系統樹の発見の物語
とにかく、ニュートンは彗星の本体は、かなり耐久力のある個体だろうと考えた。
〔そして、普遍的に、最も大きく最も輝かしいあの彗星の尾は、太陽の領域を通過した直後に発生する。したがって、彗星の加熱は尾の大きさに関係している。つまり明らかに、尾は彗星の頭や核がその熱によって放出する非常に薄い蒸気である、と私は思う〕
さらに、彗星の尾に関して、ある種の光学的な効果という説も紹介される。
〔あの彗星の尾は、彗星の半透明な頭部を通って伝播する太陽の光の影響であるという説がある……〕
彗星の尾は、光の屈折による効果のため、視覚的に認識されるか、そうでないとしても、何らかの反射物質に由来する可能性をニュートンは認識していた。しかし彼は、太陽の方向に対する見えかた、彗星軌道における尾の角度や、曲率などの計算から、彗星の尾は天空の錯覚現象でなく、具体的な物理現象と推測したようだ。つまりそれは熱で燃えている彗星の部分から発せられる蒸気。
ただ、天空の彗星を観察すると、なぜか尾は太陽の反対に伸びている。
現代では、一般的に、彗星の尾の方向が、対応の反対方向に固定されているみたいに観察されている理由として、主に太陽からの圧力が2つ考えられている。
まず”太陽風(Solar wind)”。彗星の尾の構成物質に含まれる荷電粒子が、同じように荷電粒子の流れである太陽風から影響を受けて、結果的に太陽とは反対方向への圧力になっている訳である。
もう1つの圧力が、”放射圧(radiationpressure)”、あるいは単に”光圧(lightpressure)”と呼ばれるもの。光が物体に吸収か反射される際、(おそらく運動エネルギーの交換のために)物体表面におよぼす圧力。
問題は、ニュートンの時代には、電磁波(光)に関する、数学空間で使えそうな理論がほとんどなかったことだろう。それでも、今のと似たような考え方がすでにあったのは間違いない。
〔ケプラーらは、尾が太陽の反対に進むのは、尾の物質を運び去る光線の作用によるものであると考えている。自由性の高い天の空間においては、光線の作用も大きくておかしくない。
別の人は、軽い粒子と重い粒子の両方があり、尾の物質はその軽さによって太陽から上昇していると考えている。
しかし、地球上の天体の重力は内部物質のようなもので、保存されている物質量により、集中したり解放したりすることはないようなので、この上昇はむしろ尾の物質の希薄化から生じているのでなかろうか〕
それから、ニュートンは、具体的な自説を書く。
〔……熱により希薄化したこの空気は、比重の減少により上昇し、混合された煙を運ぶ……
粒子は、その反射作用により加熱され、それらが含まれるエーテル状空気を加熱する。それはそれ自体に与えられた熱によって希薄になり、以前は太陽に向けられていた比重の減少により、太陽の尾と大気を構成する反射粒子を伴って上昇する〕
しかし、ニュートンの言うエーテルとは、何のことだろうか。今ではこの名は、光波の媒介である、宇宙全体に広がる謎の要素(とてつもなく薄い空気みたいなものか、あるいはダークマター的なもの)としてよく知られる。あるいは、もっと古くから仮説としてあった、地上の物質を構成する4つの元素(火、水、土、風)とは違う、天空世界に関連している第五元素のこと。
ニュートンの世界観でも同じようなものだろう。ただし、ニュートンは、光が波でなく粒子である説に傾いていたから、それは光波の媒介ではないはずだ。
先の万有引力、それに熱の原因と合わせて考えると、より興味深いかもしれない。
さらには、彗星の尾が気化した部分、つまりある種の蒸気である場合、当然ながら、ある疑問がある。つまり、動く彗星の蒸気尾が、その構成粒子すべて、ひたすらずっと彗星についたままであるか、という疑問。
もちろんニュートンは冷静で、そのような不可思議なこと(彗星となった素材群は、その後に溶けようが、動こうが、圧力にさらされようが、この宇宙で、決して、集合構造をわずかでも崩すことが絶対ないというようなこと)が普遍的である世界観など、はなから考えてもいなかったようだ。
ただ、そのような気化した彗星の部分(尾)から、放出されるもののに関しては、また興味深い説を考えている。
つまり、ニュートンは、そのような天体の構成素材の一部が気化した場合、蒸気が、やがて宇宙空間に拡散して、重力により引き寄せられ、惑星の大気と混ざるシナリオを考えた。惑星(地球は重要な例だが、ニュートンの時代には、まだ太陽系の他の惑星にも、地球と似たような環境がある可能性も十分にあるとされていた。ニュートンが、地球以外の惑星も同じようなものだと考えていたかは、よくわからないが)の天候のシステムも、同じような理屈で説明しやすいが、ニュートンはそこに生命の謎も絡めている。
〔……太陽の熱は、海を気化し、蒸気は雲の中に追い込まれ、雨となってまた降り注ぎ、野菜のための灌漑と栄養を地上に与える。あるいは、山の寒い頂上で凝縮して泉や川に流れ込む……凝縮した蒸気は、植物や腐敗によって消費され、乾燥した土に変換される液体が何であれ、継続的に供給され、更新される可能性がある……
おそらく、乾燥した地球の容積は絶えず増加しており、液体は、他の供給源から増加しない限り、継続的に減少し、最終的には機能しなくなる〕
そして注目すべきは、やはり生命の起源に関してだろうか。
〔私はさらに、空気中の最も小さな部分ではあるが、しかし最も繊細で優れており、万物の生命に必要とされる魂(spiritum)が、主に彗星から来ているのではないかと疑っている〕
現代風に言うと、ニュートンの彗星魂起源説は”パンスペルミア説”というやつ(つまり生物構造の起源が、地球外にあるという説)だろうか。それはそうかも知らないが、しかし現在、生命の起源を宇宙に求める場合、たいてい宇宙からもたらされたものは、アミノ酸とか、ある種の分子情報とかであって、普通は魂ではない。
ただ、魂というものが、具体的にどういうものであれ、ニュートンの宇宙での(少なくとも)彗星の尾に関しては、ある種の化学反応の結果のようだから、そこでの魂は、(特別に世界に神が与えたものとかでなく)物理的現象により生じたものと思われる。それこそ、(現代よりまだかなり神秘的だった)熱とか電気とかが、つまり魂というものの正体だった説を考えていたのかもしれないが。
光学。色の謎を解明するための様々な実験
ニュートンの著作の中で、『光学』という本は、おそらくプリンキピアに次いでよく知られている。そしてこの本もまた、プリンキピアと同様に、その構造的には、エウクレイデスの原論的である。
この本は、タイトル通りに光の謎と、その研究成果について書かれているが、プリンキピアと比べると、理論的考察の他、実験結果の報告がかなり多いのが重要な特徴であろう(全体的には、『色彩学』というタイトルだったとしても違和感がないくらいには、色の話題もかなり多い)
おそらくニュートンとしては、こちらの方がかなり身近なもの(あるいは世界の中での小さなスケール、わずかな部分)を扱っているつもりだったと思う。
古典世界の光学研究
やはり、最初に定義と公理がくる。以下で、いくつか、そこでの興味深い記述に関して考えてみる。
〔定義1=光の射線とは、光の最小粒子であり、異なる直線上で同時に存在するばかりでなく、同一直線上に連続的に存在するものとする。
このように、光が連続的に存在する粒子と、同時に存在する粒子の双方からなることは明らかだ、同じ場所で、ある瞬間にくるものを止め、すぐ次にくるものを通すことができ、また同時に、ある場所でそれを止め、他の場所で通すことができるからである。止められる光の粒子は、通される光の粒子と同じではありえない……
定義2=光の射線の屈折性とは、ある透明な物体または媒質から、他の透明な物体または媒質へと進む時に、屈折、または道筋を変える性向のことである。射線が大きな、あるいは小さな屈折性とは、同じ媒質に同じように入射しても、その道筋を大きく、または小さく変える性向のこと。
数学者たちは、光の射線を発光体から照らされる物体にいたる直線と考え、また射線の屈折を、一つの媒質から他の媒質への進行の際のそれらの直線の屈曲または屈折と考えるのが普通だ。確かに、もし光が一瞬のうちに伝播されるものならば、射線と屈折をこのように考えることもできる。しかし木星の衛星の食現象の時差から得られた論証によると、光の伝播には時間がかかる。したがって私は、いずれの場合の光にも当てはまるように、射線と屈折を一般的に定義することにした〕
光の射線(光線)、この現象だけを考える時、以下の3パターンのものが見られる。その光線をすっかり途切れさせる、不透明なもの。光にとってほとんど無視できるようである透明なもの。ある程度光を通すが、通過後の量をある程度減らしているようにも見える、中途半端に不透明(半透明)なもの。
また、不透明な物質を光の光線で閉ざした時、閉ざされる前の不透明な物質の向こうの光、それが粒子の集合体であるならば、粒子群は一瞬で消えているのかどうか。普通に考えるなら、この閉ざされた瞬間に消えるというのは、光があまりに早すぎて、閉ざされた先の切られた粒子群は全て、先に進んでなくなってしまっているかのように見えるだけなのかもしれない。だがそうなると、光の源から放たれる光の粒子群は、常に超高速で先に進んでいるわけだから、例えば細い光線でも凄まじい数の粒子が含まれているかのようだ(ニュートンもいくらか指摘したように、それはまた別の問題を抱えているわけだが、エーテルを媒体とする波動説だと、粒子の場合のような異常な数の問題はあまりない)。
定義1で出ている、光線は、同一直線上に連続的に存在する粒子でもあるという考えは、わりと重要なのかもしれない。また光線をいくつもの線の集合と考えれば、様々な直線上にそのような光の連続的な流れがあることになるが、ある場合に閉ざされる連続と、閉ざされない連続があるなら、それらに何らかの区別があるかもしれないと考えるのも、無理ないだろう。
屈折性に関しての定義2では、さらに光に速度があるということの実験結果も紹介されている(有名なレーマーの実験であろう)。このことは粒子数の謎を大きくしているようにも思う。光が粒子なのだとして、大量に存在しているそれは何か。
光線が何であれ、有限速度で動いているように観測される、連続的なものであるだろうか、というのは現代でもなかなか面白い問いかけであろう。
現代において光というのは、”可視光”と呼ばれる、ようするに目に見える波長の電磁波である。そして電磁波というのは、空間内の電子(または荷電粒子)の動作のために生じた電磁場と磁場が相互作用を繰り返していく結果の波とされている。非常に重要なことは現代のこの考え方は、数学空間による現象の解析における様々な前提や数値や変化を、現実の要素の言葉で定義したようなもの(場とか波とか)であるということだ。
ただ、光は単に波というだけでなく、実験や観測の方法によっては粒子のように振る舞う。しかも、そのような粒子と波の(普通は、今でも奇妙と呼ばれる)二重性は、様々な微小な粒子の典型的な特徴でないかともされている。もちろんそのような二重性も、数学的な分析結果の産物(1つの解釈。ただし、他にどのように考えるべきか)である。
特に、現代物理学における「場」と呼ばれるものは、経験的な世界観の中で深く考えてみると、たいてい、それ単体でかなり奇妙な概念である。それには色々な解釈があるだろう。1つの典型的なものは、例えば、ある力の作用範囲。世界全体の空間というより、空間の中である力の影響力が機能することができる、空間内空間のようなもの(実際的に、数学空間においてのイメージ的には、そのようなものと考えていいと思う)。はっきり言ってこの概念が現代物理学においてなくてはならないものとされているのはその存在せん存在の現実性よりもそれが存在すると考えた場合の実用性のあまりの大きさだ。場は、世界の動作を考えるのに非常に便利な概念なのである。
ただし、ニュートンの時代にはまだ、場という概念は一般的じゃなかった。だから、何を伝える媒介としての場を想定することが普通はできない。結果的に、エーテルのようなより実在的な何かを考える必要があった(だが、場を、エーテルと同じくらい実在的に考えても大丈夫かもしれない)。
電荷(というより荷)というのは、世界の物質群を細かく分解していった時に現れると思われる、粒子自体が抱えている力。としても、これも謎は多い。それははたして、世界全体のシステムの中で、文字通り「力」と定義できるような要素か。それとも実は、物質が抱えている「(真の)力」と、現実の世界の影響のネットワークとの媒介のようなものであるのか。
今の我々は、ニュートンよりどれくらいのことがわかっているか。彼は場という概念をおそらく知らないで、そして光が波でなく粒子であると考え、光線を連続的な粒子群とも考えた。
だが、数学的な分析は洗練され、光に関する観察結果のデータも増えたのは間違いないが、現実に起きる解釈の精度は、どのくらいか変わったろうか。
〔定義7=射線がすべて等しい屈折性をもつ光を、私は単純、均質、同質とよぶ。また射線のあるものが他のものより屈折性が大きい光を、複合、不均質、異質とよぶ。
私が前者の光を均質とよぶ理由は、それがすべての点に関して均質であるとためでなく、屈折性の等しい射線は、これから論じていく様々な諸性質も等しいからである〕
この定義7は、決定的実験との関連が深い。つまりニュートンは屈折の異なる様々な光が合わさったものと思われた白い光線を、道具を使って実際に(屈折率ごとに)ばらけさせた、色の異なる様々な光を確認した。現代的な解釈によると、各光線の波長の違いのための区別の定義。
ちなみに、光学における、最初の命題1定理1は「色の異なる光は屈折性の度合も異なる」というもの。
〔公理7=任意の対象のあらゆる点からくる射線が、反射または屈折によって収束させられたのちに、再び同数の点で出会うところではどこでも、その射線が落ちる任意の白い物体の上に、その対象の画像を作る……
人が任意の対象を見るとき、その対象のいくつかの点からくる光は、眼の透明な被膜と体液(すなわち、角膜とよばれる外被膜と、瞳孔の背後にある水晶体)とによって屈折され、収束して眼底の同数の点で再び集まり、眼底を被っている(網膜とよばれる)被膜に対象の画像を描きだす。なぜなら解剖学者は、硬膜とよばれる、外側の最も厚い被膜を眼底から除去したとき、薄い被膜を通してその上に生き生きと描かれる対象の画像を見ることができるからである。そして視神経の繊維に沿った運動によって脳へと伝えられたこれらの画像が、視覚の原因であろう。なぜなら、これらの画像が完全であるか不完全であるかに応じて、対象が完全に、または不完全に見られるから。
もし(黄疸などの時のように)眼に何らかの色がつき、眼底の画像がその色になると、あらゆる対象はそれと同じ色に見える。
もし眼の体液が老齢によって減少し、収縮のために角膜と水晶体の被膜が以前よりも扁平になると、光は十分に屈折されず、このため眼底ではなくて、その背後のどこかで収束することになるが、結果、眼底には混乱した画像を描き、この画像の不明瞭さに応じて対象は混乱して見える。これが、老人の視力の減退の理由であり、また眼鏡によってなぜ視力が回復されるかも示している。なぜなら、凸レンズは眼のふくらみの不足を補い、屈折を増すことによって射線をより早く収束させ、もしレンズの凸の度合が適当であれば、眼底に明瞭に射線を集めるからである。眼がふくらみすぎている近視の人では、反対のことがおこるのだろう。その場合、屈折が大きすぎて、射線は眼底に到達しないうちに収束して集まるからである〕
ニュートンの著作全体を通して、それほど数が多いわけではないが、いずれもたいてい興味深いものである、ある生物というシステムの機能に関連している部分。
光を捉え、さらに光を放った対象の形を識別するための構造のほか、神経の動作を介して脳に伝わる画像情報(識別された物体の形)の処理についても推測されている。
ここで、何か物事を理解する意識というものをどう考えるか。現実の動作とそれを処理しているというシステムをどのように考えるか。によっては、かなり唯物的な世界も想定できるかもしれない。
ニュートンの場合は明らかに違っていた感じである。少なくとも、物質世界と物質世界における情報処理システムの、こういう考察のみをピックアップし、彼を偉大な唯物論学者のように語るのはおかしい(そんな人が実際いたら、ひどい歴史修正主義者と言えると思う)。
意識の原因は、例えば魂と呼べるようなものだとして、そうすると、感覚器官(例えば目のような構造)がとらえた、外部の物質情報を処理する、脳という物理的構造を、どう考えるべきか。それこそ、まるで物質世界と非物質世界の媒介となる物質構造のようだが。
 「意識とは何か」科学と哲学、無意識と世界の狭間で
「意識とは何か」科学と哲学、無意識と世界の狭間で
感覚は幻想であるか
〔命題2定理2=すべての均質光は、その屈折性の度合に応じた固有の色をもっている。その色は反射と屈折によって変化させることはできない。
……実験により、私が不均質射線を分離した時、分離された射線によって形成されたスペクトルは、最大屈折性の射線が落ちた一端かから、最小屈折性の射線が落ちた他端まで進むにつれて、董、藍、青、緑、黄、橙、赤およびそれらの中間のすべての色の一連の色に彩られ、たえず変化する連続的系列として現われた。ゆえに屈折性の異なる射線の種類と同数の色の度合が現われたと考えられる。
実験5=……これらの色が屈折によって変えられないことを、私は、光(均質光)のきわめて小さな部分を、またときには別の小部分をブリズムで屈折させてみて知った。この折、光の色は全く変化しなかった……
実験6=これらの色は屈折によって変えられなかったように、反射によっても変えられなかった……
私はまだ、均質光を反射し、その色を感知されるほど変えることができた物質を見たことがない。
これらから明らかなことは、もし太陽の光がただ一種類の射線だけからなっていたとすれば、全世界にはただ一色しかないであろうし、反射と屈折によって何か新しい色を生じさせることもできないであろうこと。したがって、色彩の多様性は、光が複合されたものであることによる〕
ニュートンの時代には、光の色は、屈折や反射のような物理現象の影響を受けて、光が帯びる要素という説があり、それの否定でもある。
ただ、光に色という要素が与えられるにせよ、光そのものに色があるにせよ、そもそも色というのはいったい何か。
〔……私が光や射線に色がある、または色を付与されているというとき、それは哲学的に、また厳密にいっているのではなく、大まかに、普通の人々がこれらすべての実験をみていだくであろうような概念に従って言っているのであると理解されたい。なぜなら、厳密にいえば射線には色などついていないだろうから。それらの中には、あれこれの色の感覚を惹きおこすある能力と性向があるだけであろう。なぜなら、音は、鐘、または楽器の弦、または他の音響を出す物体の中では、震動以外の何物でもないのに、また空気中ではその対象から伝播された運動以外の何物でもないのに、感覚中枢の中では、それは音という形態での、不可思議な感覚であるからである。
色も同じようなものだろう。それは対象の中で、あれこれの種類の射線を、他の射線よりも豊富に反射する性向以外の何物でもない。射線の中では、それらはあれこれの運動を感覚中枢に伝える性向以外の何物でもなく、そして感覚中枢ではそれらは色という形態での感覚である〕
音と色は、現実の要素というより、世界のある部分を認識する人間の感覚上の、いわば理解のために、変化する数値(ある種の変数)として定義されたデジタル要素みたいなもの。それがニュートンの結論だったのだと思う。
 「視覚システム」脳の機能が生成する仕組みの謎。意識はどの段階なのか
「視覚システム」脳の機能が生成する仕組みの謎。意識はどの段階なのか
現実とはいったい何だろう? 我々の意識は、バーチャルを介さないと、本当の世界を認識することもできないのだろうか。だが、そうだとすると意識(あるいは魂)とは、いったい何なのか。
ドレミと色。どこまでがバーチャルであるか
ニュートンはあちこちで、音の比と、(屈折率の異なる、あるいは色の違う、または現代的に言うなら波長の異なる)光の比に関して、やたらと関連付けたがっているような印象がある。実際、そのようなものがあると前提にしている印象の実験もいくらかある。
それは、例えばピタゴラス的な数学的世界(本質的に世界の全ての要素は、ある種の数学法則に縛られている世界)というよりも、おそらく人間の認識の方法を踏まえてのことだろう。
つまり、人間は世界をバーチャルというか、デジタル的に理解している節がある。視神経が何かを理解するのに、ある種の数字の法則に変換するというのなら、音と光のような、現実の宇宙においては別々と思われるような現象を、似たようなものとして考えることは可能である(つまり数学的に、同じ概念に当てはめられる別々のものを、同じ概念として考えることが可能)。
色のシステム。虹を見る時、世界を見る時
〔命題7定理5=光によって作られ、想像力に依存しない宇宙のすべての色は、均質光の色かまたはそれらの複合……
……あらゆる種類の射線が集まり混ざり、白色がつくりだされる……まさに白はすべての色の中間で、他のどれにも偏っていない。なぜなら、白はいずれの色でも、等しく容易に彩られるから。例えば赤の絵具に少量の青を混ぜても、あるいは青の絵具に少量の赤を混ぜても、すぐには元の色を失わないが、白の絵具に任意の色を混ぜると、すぐに混ぜた色になる。
太陽の光はすべての種類の射線を混合したもので、その白さはすべての種類の射線の色の混合……それらの射線は、いつどのような屈折または反射を受けようと、つねに変らずそれらの固有の色を保持する……
……私はここでは光から生じる色に限って述べる。なぜなら、色は他の原因によっても現われることがあるからだ。たとえば幻想の力によってわれわれは夢の中で色を見れる。また狂人は眼の前にないものを見る……しかし他の原因が介在していないところでは、色は光を構成する一種、もしくは数種類の射線につねに対応している……〕
色は感覚であるから、光だけが原因とは限らないのだろう。例えば脳という構造が部分的に損傷(?)して、他の人が青色を感じる光の情報を処理した時に、赤色を感じたりもありえるだろう。それどころか、他の人が食べ物を食べて美味しいと感じる時に、色を感じることもあるかもしれない。
しかし、白が究極的に中間的な色であるというのが、世界(あるいは人間の知的構造)の標準だろうか?
命題9問題4「発見された光の諸性質によって虹の色を説明する」でニュートンは、自分以前の、”虹(rainbow)”に関するいくらかの研究にも触れている。
ニュートンの時代には、虹の原理自体は、かなり一般的になりつつあったようである。〔太陽の光が降る時、大気の雨の滴の中で屈折することによって生じると、認められている〕とニュートンは書いているが、この説明は、簡潔なものとして、現在でもそのまま使えると思う。もちろんニュートンも、厳密には太陽と雨が必要なのでなく、光と水が必要であって、人工的に虹を作ることも可能だと、しっかり理解している。
光と、色と、そこに生きる知的構造。総体として非常に複雑である、そんな世界観がここまで(現実において安定して)うまく機能しているのは、まさにクリエイターが存在するからでないかとニュートンは推測した。
しかし特に、ダーウィン進化論が一般的になって以降は、世界に存在する理由など本当にあるだろうか? 何かの目的がなくても、長い時間での世界の変化は、どこまでも複雑になることも可能でなかろうか。という考え方も強くなっている(このことは、現代人たちからすると、驚くべきほど簡単な話のように思えるかもしれない。実際、ニュートンの時代、それに彼の時代よりも以前にも多くの唯物論者が、そんな感じのことをちゃんと言っていた。それでも、人々の集団の中での常識というものは、常識となるまではマイナーだ)
 「ダーウィン進化論」自然淘汰と生物多様性の謎。創造論との矛盾はあるか
「ダーウィン進化論」自然淘汰と生物多様性の謎。創造論との矛盾はあるか
ただし世界が、ただ存在するだけな場合と、そこに、そのような存在している世界を理解できる存在(知的構造)がある場合を比べたらどうだろう? 実際、複雑なのは複雑だと理解する者たちの方と考えることもまだ可能と思う。いわゆる人間原理のような話になってくるが、複雑なパターンを理解できる存在は、複雑なパターン上にしかそもそも存在できないかもしれない。
しか、複雑な世界でしか存在できない何かのために、この複雑な世界を設計したクリエイターがいるとする。でもそのクリエイターは、例えば感覚的なものである色とかを、どうやって設定したのか。それがどういうものか、それにはわかっていたのだろうか。それとも、そのようなものが生み出せる理論とか持っていたのだろうか。
本当に、全てが意図的というのは、逆にありえるのだろうか(時に、色々な物語におけるクリエイターとしての神は、この世界にしばしば予想外のものを見出しているが、それはそういう存在が真の意味で全て支配している決定論的世界観が、物語の舞台として扱いにくいからだろう)。
色付いた世界とは何だろう。
クリエイターと、神学的パラレルワールド
光学は、特に序文において、「まだ出版するつもりはなかったが、周囲の人たちに強く説得されて、結局世間に出すことになった」とか書いている。実際に、これは未完成の書だとして、最後にニュートンは、いくつもの未解決の疑問をあげている。それは、単に光とか色とかの疑問だけでなく、光とか色とかいう要素が存在しているこの世界そのものの全システム構造に関する疑問にまで至っている。
例えば、重力とか電磁気の引力、その他にも存在しているかもしれない自然界の未知の力。そのような力が、自然世界の物質構造の大部分をつくっているかもしれないという推測。それがある程度正しいなら、自然世界の中のそのような力、またはその原因が機能するためのネットワークがあるのではないか、という疑問。
また、最小の粒子は、最も硬く、そしてそのような小さな粒子が結合してより大きな粒子を作るが、そのような複合粒子は結合前よりも基本的に弱くなるのでないか。そしてそのような結合プロセスはある段階で止まるが、そこで安定した複合粒子群こそが、物体の様々な性質を決定づけている素材物質なのでなかろうか、という疑問
さらに、代数学で正の量が消滅するところから負の量が始まるように、力学でも、引力が終るところから発生する斥力があるのでないかという疑問。興味深いことにニュートンは、光の反射現象の他、化学反応による物質粒子の分解も、そのような実在的な斥力による現象の例としている。つまり、物質の運動量が熱によって高められるために粒子がばらける、というより、物質粒子を引き付け合う力が、熱によって何らかの変化を加えられ、斥力に変換されてしまう、というような見方であろうか。
そして、流体の粘着性、粒子の摩擦、固体の弾性などの影響で、運動量は常に失われるようだが、そうして常に減少し続ける世界の様々な動作を、回復させる能動的動因があるのでないか、という疑問。重力や電気や磁気、それに化学反応などは、そのような、物質動作を(少なくとも世界の存続期間の間)永遠に機能させるための世界システムの一部なのでないかと。
さらにニュートンは、上記のことをまとめて、この世界のクリエイターとしての神の方法をも推測する。
曰く〔私には次のことが確からしく思われる。すなわち、初めに神は物質を、充実して、密で、不可入性の、しかし可動の粒子群として形作った。その大きさと形、その他の性質および空間に対する比率は、神がそれらを形作った目的に最もよくかなうようにされた。その始原粒子は決して磨滅したり、壊れたりしないほどきわめて堅い……
始源粒子が壊れず完全であるかぎり、それらは万世を通じて同じ性質と構造をもつ物質を構成することができるだろう。仮にそれらが磨滅したり、粉々になったりすると、それらに依存している事物の性質も変るにちがいない……したがって、性質が永続的であるために、有形物の変化はこれらの永久粒子のさまざまな分離と、新たな結合と、運動とにのみもとづかなければならない……
さらにまた、これらの粒子には慣性力があり、その当然の結果である受動的な運動法則を伴うばかりでなく、ある能動的動因、たとえば重力とか、発酵とか、物質の結合をひきおこすような動因によっても動かされていると私には思われる。これらの動因は、事物の特殊な形態から生じるとされている隠れた性質ではなくて、事物そのものを形成する一般的な自然法則であると私は思う……〕
しかし、そもそもクリエイターなどいるだろうか。ニュートンはいる方が合理的だと考えた。
星系とか、生物構造の、見事というほかないデザイン性こそが、そのような賢きクリエイターの強力な証拠なのだと。
もう一つ。ニュートンは、別の世界の可能性も考えたようだ。つまり神が、他の世界を創れた可能性、あるいは創っている可能性。
〔空間は無限に分割することが可能であり、物質は必ずしもあらゆる場所には存在しないのであるから、神が物質粒子を、さまざまな大きさと形に創り、空間に対してさまざまな比率にし、またおそらくそれぞれ異なる密度と力をもたせることができ、そうすることによって自然法則を変え、宇宙のそれぞれの部分に、異なる種類の世界を造りうることを認めてよいであろう、少なくとも、私はこれらすべてに何の矛盾もないと考える〕
こういう考えは神学的パラレルワールドと言えよう。ただし、このパラレルワールド仮説は、現代における神の存在しない世界観でのパラレル宇宙よりずっと、繋がることが可能であるかもという希望が大きいと思う。
錬金術論文。隠された物の真理の探索
ニュートンが、錬金術に関して残しているテキストのほとんどは、錬金術師の書いた書物からの引用と、それのちょっとした考察みたいなものだ。
 「錬金術」化学の裏側の魔術。ヘルメス思想と賢者の石
「錬金術」化学の裏側の魔術。ヘルメス思想と賢者の石
むしろ、彼がよく試みていたのは解読に近い。
『Epistola ad veros Hermetis discipulos continens claves sex principales Philosophiæ secretæ’(秘密哲学の6つの主要な鍵を含むヘルメスの真の弟子たちへの書簡)』にはこうある。
〔重要なのは、私たちの仕事の主題である真の素材(materiamveram)を見つけることであり、そのためには、それが隠されている千の曖昧な言葉を理解する必要があるからです。そのすべての特性を理解し、芸術がそれに与えることができる完璧さの程度を判断する必要があります〕
実際、多くの錬金術文書は、意味が曖昧な記号や、明らかに字義通りに受け取るものではない言葉に溢れている。例えば「ディアナのハト」とか、「緑のライオン」とか、「翼を有するドラゴン」など。
ニュートンは、聖なる書物の予言などに関して、「曖昧な言葉をそのまま読むのでなく、そこに隠された真の意味を解釈することが大切だ」というようにも書いたが、錬金術に関しても似たようなスタンスだったのかもしれない。
生命の素材、魂の抽出実験
ニュートンは、物理数学系の考察では、その正体を理解できないと諦めてた節がある。魂(神秘的な非物質的存在)を、錬金術の研究資料に探していた節がある。
実際、ニュートンがそのようなオカルト話を、どのくらい真に受けていたのかは謎だ。ただ単に、彼の時代においては、世界に存在すると思われる非物質的な本質的システム要素を、具体的に理解する術として、数学よりオカルトの方が可能性が高いと考えただけかもしれない(多分、現代でもそういう人はたくさんいるだろう。そして、ニュートの時代ではそういう考え方は、今よりずっと一般的だったと思われる)
しかし例えば、『発酵による「哲学的水銀」の調製と「ダイアナのハトの仲介」、「月経」の調製などに関するメモ。(Notes on the preparation of ‘philosophical mercury’by fermentation and ‘ye mediation of Diana’s Doves’, on the preparation of ‘menstrua’, etc)』に見られる記述。
〔私たちの粗末な精子(crudesperm)は3つの物質から流れ出し、そのうちの2つは、3番目によって生成する大地から抽出され、その後、私たちの汚れた婦人の月経から引き出された純粋な乳白色の聖母のような性質になる。
3つの源泉とは、水(外側の殻が届く限り、詭弁家が見ることができる水銀の結合)、血(完全に揮発性で金属質を欠いた緑のライオン)、精神(狂気的な姿で世界に現れる混沌)である。小さな形で、私たちの、緑のライオンの血と繋がった哲学者に捧げられ、それにより、この種のすべての生き物を貪り食うことができるライオンになる。
精神は水と血から分離可能であり、その時、私たちのライオンは、実際には緑だが、そのとき私たちのライオンではなくなり、真の構造体たるエメラルドとなる。そして水という泉はすべての人がくみ、多くの人が利用する共通の井戸である〕
こんな記述をどう理解すればいいのか。確かにこれは、とても曖昧で、どうとでも解釈しやすい。ただし、一般的な錬金術のイメージに則って、だいたいこういうことだろうと典型的な推測をすることはできるかもしれないが。
つまり、上記の例でいうと、生物行動の源となる液体である精子は、主に水と血と精神(魂)から成る。基本的に精神は、水や血に付属されてるように存在するのが普通だが、切り離すことはできる。その場合、血はその構造体としての本質的な物質である緑色のエメラルドに変化するはず。一方で水は、この世界の中でありふれていて、様々なことに汎用的に利用できる素材物質。というようにでも考えればいいのだろうか。
賢者の石は、最初の物質か
錬金術における究極の目的と言えば、やはり”賢者の石(philosophers’ stone)”であろう。それは実際には石というより霊薬ともされ、様々な物質を変換する化学反応の触媒になるとか。
また、”エリクサー(elixir)”と呼ばれる、生命体に不老不死をもたらす霊薬も、ある種の賢者の石とされる。あるいは、それらは同一視されることも多い(多分、ニュートンも普通に同一視していた)。
賢者の石に関すると思われるニュートンの記述としては、例えば『さまざまな化学プロセス(分離、行列、昇華、蒸留など)に関するメモ(Notes on various (al)chemical processes(separations, processions, sublimations, distillations, etc))』の、以下のようなものがある。
〔……それは万物の根元的な水分と生命、不燃性の水分、燃えない油、大地が生み出す空気、万物を温め栄養を与える消えることのない火、塩は脂肪で乾燥しているが、非常に湿っているのですべての根源である。宇宙の塩辛い液体。それこそ正しく、私たちが石と呼ぶ液体。
優れたエリクサーを作ろうとするなら、それを均質な油状物質に変える必要がある。最後に、これらの液体は純粋なものに変換される……
もし私の愛する人の両親(すなわち、太陽と月の固定された地球の人々)が、(別々に浸し、乾燥させることで)命の水の味を味わい、(もう一度浸し、乾燥させることで)私の乳で栄養を与え、私の白に酔う(材料が完全に白くなるまで飲む)、そして私のベッドで結婚する(つまり、それらが楕円形のガラスの容器の中で混ぜられる)なら、彼らは月の息子を生み、その息子は彼のすべての親子との繋がりを持つ(太陽と月はお互いに消えないから)。そして、私の愛する人(つまり、長老の近くの賢者の金である白くなった土)、赤い岩の流れから(つまり、太陽の油で)、そして(別の飲酒を通して)彼の母親の春を味わい、それから私の赤ワインに加わり、(飲酒によるすべての影響が大地に変わるまで)私のベッドで私と一緒に酔い、友好的に一緒に寝ていました。つまり私は妊娠する。そして私の時代には、地球上のすべての王や王子たちを支配し統治する最も強力な息子を産む。勝利の黄金の冠を戴く〕
やはりわかりにくいが、他の文献にも書かれた、様々な、錬金術実験による物質変換の話と合わせて考えると、多分ニュートンは、『光学』とかで言及していた、(神が世界を創った時に、最も基本的な素材として最初に造ったと思われる)万物の基礎となる不滅の粒子と関連しているものとして、賢者の石、あるいはそのようなテクノロジーの可能性を推測していたのでなかろうか。
だからこそ、第一素材が重要なわけである。まさにこの物質世界の万物に関して、その全ての変化の鍵となるものが、その世界の第一素材と期待していたのでなかろうか。
ダニエルと黙示録の考察
ニュートンの科学的探究と、錬金術の書物の研究は、分けて考えられることもあるが、実際は結構結びついてるような印象がある。
では、(ニュートンが熱心なキリスト教信者だったというのは有名であるが)神学的興味と、他との関連はどうだろうか。
人間の考えた知的体系(つまり数学、幾何学)による分析が科学研究。数学分析上は正体のわからない世界要素を、ある程度適当に決めた場合の世界研究が錬金術。としたら、神学研究はどういうものであったか。
それは予言の言葉。霊感により人間に与えられ、言葉として表現された、神の何らかの意図を読み取るため。そんな印象も少しある。
ニュートンによる『ダニエルと黙示録の考察』は、タイトル通り、聖書における2つの書物、ダニエル書と黙示録に関する考察がひたすら書かれた本である(曰く、ダニエルは、時系列などの問題点を考慮すると、最も理解しやすい予言。そして黙示録は、多くの人々が最も強い興味を抱いてきた予言だとか)。
具体的には、そこからどんなことが読み取れるか。
 「新約聖書」神の子イエス・キリストの生涯。最後の審判の日の警告
「新約聖書」神の子イエス・キリストの生涯。最後の審判の日の警告
聖書はどのように成立したか
そもそも、なぜ聖書を信じるのか。神を信じるとしても、この、いくつかの文献のよせ集めを信じる必要はない。
ただ、1つ重要なことは、ニュートンの時代には、この宇宙がどのくらい続いてきたのか(少なくとも、どのくらい過去があったのか)に関して、実質的に、ほとんどまともな手掛かりがなかったことと思う。
現在は、宇宙の始まりの時を説明する仮説として、ビッグバン理論が主流だ。あるいは、その理論を信じていない場合ですら、この地球という惑星が、宇宙ができた時から存在している惑星というのは考えにくくなっている。また、この宇宙が誕生した時にすでに地球が存在していたとしても、地質学的な様々な研究成果が、この地球という惑星に人類が誕生したのが、全体の時間の中のごく最近ということを示唆している。結果的に、古いほとんどの神話に見られる(聖書にも見られる)神が世界を創って、人類を創った、というような記述が、はなから奇妙になってしまう。
 「ビッグバン宇宙論」根拠。問題点。宇宙の始まりの概要
「ビッグバン宇宙論」根拠。問題点。宇宙の始まりの概要
もちろん、それは考え方の問題かもしれない。しかし普通、詳しく説明されないと、例えば神が世界を創ってから、それから何十億年経ってから、人類を創った。または、進化論というシステムが機能するような世界を創ってから、最初の単純な生物を地球に置いた、というようなシナリオ、あまり考えないだろう。
とにかくニュートンにとっても、他の多くの西洋の神学者らと同様に、聖書は重要な研究資料だった印象である。
では彼は、この書物が、この世界でどのように成立したと考えていたか。
ニュートンは聖書の各所の記述(登場する歴史人物とか、引用の範囲とか)を手がかりに、いくつかの書について、どこの誰がいつ書いたのかを考察した。
特に興味深いのは、中途半端な理解や解釈違いによって、神の教えを外れてしまった民族の話とかだろうか。そういうことがあるからこそ、予言の真の意図を理解することが重要なのであるというような。
〔評議会、会議、司教、長老の権威は人間によるものです。預言者の権威は神聖なものであり、モーセと使徒を預言者の中に数えると、宗教の総体となります。そして、もし天からきた天使が、彼らが伝えたもの以外の福音を説教するなら、彼は呪われるだろう。
彼らの著作には、神とその民との間の契約と、この契約を守るための指示が含まれている。それを打ち破る神の裁きの例と、今後の出来事の予測もある。
神の民は契約を守っている間、神の民であり続ける。契約を破ると神の民でも教会でもなくなり、自分たちはユダヤ人であるのにユダヤ人ではないと主張するサタンの民となる……
これから起こることの予言は、あらゆる時代の教会の状態に関係している〕
神の計画上の国家
〔……4つの金属で構成される、時代のビジョンの中に、ダニエルのすべての予言の基礎が築かれている。それは、地球上に引き続き君臨すべき4つの偉大な国家の集合体を表している。つまり、バビロニア、ペルシア、ギリシャ、ローマの人々。
手を使わずに切り出された石が、像の足元に落ち、四つの金属をすべて粉々に砕き、大きな山となり全地を満たした。それはさらに、4つの王国の後に新しい王国が生じ、それらすべての国々を征服し、非常に大きく成長し、すべての時代の終わりまで存続することを表す。
像の頭は金でできており、ダニエル自身が解釈しているように、最初に君臨したバビロニアの国々を表している……〕
予言者が、どういう原理でか、見ることのできた、未来に関するビジョン。それが正しくないなら、話はそれで終わりだがもし正しいのならば一体未来を見るとはどういうことかそれは変えられない未来であるのなら予言の意味はあまりないあるいは予言というのはあるいは予言というそのものが運命によって作られることが決まったもの。
全ての時間の因果関係に変更を加えることができないから、その意味で、予言は未来に向かう人類の、対策の道具としては何の役にも立たないことになる。
もし予言が存在することによって、未来において真に救われるべき者たちが、救われる準備を整えることができるというのなら、それでも結局、変えることのできないシナリオ(神の意図)が最初からあるのと同じ。予言を真に理解して神の存在を理解して神に救われるべき行動をして最終的に救われるという誰かは決まっている訳だ。
だが、そうでないとしたらどうか。
実際ニュートンによるいくつかの記述に、「野蛮人を無理やり神の子に改宗させることは正しい」というような考え方も見られる。それが実際、正しいかどうかはともかくとして、それは、神の道から外れてしまった者や、それを知らない者たちでも、正しき神の道への軌道修正が可能である、という前提があっての考え方でなかろうか。
またニュートンは、特に何の疑問も挟まないで、人間のある国家が、いわば偉大な1つの集合体のように、予言されていると書いた。4つの偉大な国家と。
これはいったいどういうことか。この世界の中で、国家という集合体はどういうものか。
人間のための予言であるから、人間の社会における重要なことを予言しているとでも言うのか。そうでないなら、この世界そのものにとって、人間の国家というのは、時に重要になるのだろうか。
少なくともニュートンは、物質世界のことを、数学などの人間の道具を使って分析してみた時、そこで考えた世界全体のシステムにおいて、人間という概念自体は、それほど重要でなかったはずだ。
人間のような知的生物が存在できるというのは重要な事実である。しかし、例えばその人間が、知的構造をうまく使って、国家のような社会集合体を作ったとする。だがそれは、この世界のシステム上の動作の1つであって、システムそのものとは特に関係がないのでなかろうか。
神が全てのシステムを動かしているなら、そして人間の国家とかがそれほど重要なものでありうるならば、例えば神は、この複雑な世界システムそのものを、人間や人間の社会のために造ったとでも言うのだろうか。だがその場合に、本当にこの世界のシステムが最適だったのだろうか。
それとも、人間も要素なのだろうか?
もし神が宇宙を創ったのだとして、そしてそれが計画通りのものなのだとして、小さな基本粒子の集合体が様々な物質であるように、人間もそのような構造であるように、国家というのも、ある種の巨大物質みたいなものと考えられてたりしただろうか。
ニュートンは例えば、大きな恒星の周囲を惑星が回るというような、星系システムというのは、重力などの力学的システムが(神によって)非常にうまく設計されているからでないかと推測した。実は同じように、人間の知的構造とか、それによる様々な感覚、人間の認識している、言うなればバーチャル的現実なども、つまり国家とかを作るための部分要素だったと考えたりしたろうか。
世界の最後
『ダニエルと黙示録の考察』の黙示録についての部分は、その最後の時(この世界か、あるいはある時代かはよくわからないが)と、その少し前に起こる出来事などに関連しているらしい、不思議な比喩表現の考察。
それと別に、ニュートンは、黙示録に関しての考察テキストをいくつか残している。
特に注目すべき1つが、『教皇権の台頭と黙示録の断片(Fragments on the rise of the papacy and Revelation)』であろう。
時々ニュートンは、「2060年が世界の終わりの時期」と推測したと語られているが、おそらくそれは、以下のテキストから。
〔……短命の獣の時代は、長命の王国の時代に置き換えられている。3人の王の完全な征服は、A.C.800から1260年の期間。つまりそれは主の年、2060年に終わりを迎える。
しかし、それより後に終わることもありうる。実際的には、神がご自分の胸に定めた時期や季節を知ることは私たちにはできない。
しかし私はあえてこの時期に言及した。それは、その終末時期を主張するためでなく、それより早くに(終末が)起こると予想する理由がほとんどないことを示すためだ。それにより、頻繁に終末時期を指定したがる通訳者の軽率な推測に終止符を打つためだ。彼らの悪いビジョンは実現しないから、預言は信用を失墜させてしまうかもしれない〕
おそらく、本当に世界の終わりかどうかはわからないが、しかしある時代がそこで終わる可能性は高いと、ニュートンは考えていた。
しかし、ニュートンの予言研究に関して、最も重要な問題はおそらく、物理数学の場合と違って、彼が「自分が計算したところによると」と書いて予言の時期とかを特定した時、いったいどのような計算が行われたのかが、かなり謎であることだろう。




