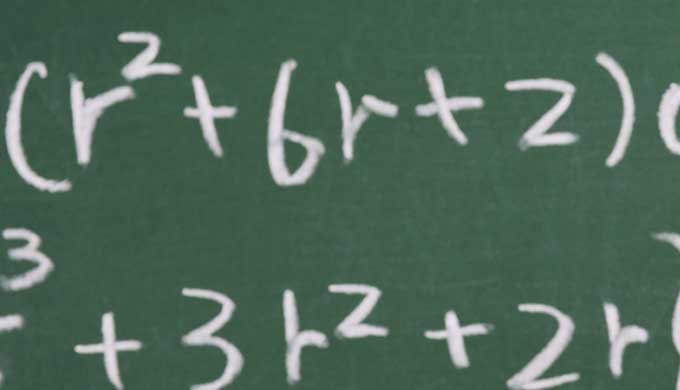ブロックの異なる増加速度の考察
目の前にふたつ、コンピューターのモニターがあることを想像しよう。
どうも、どちらのコンピューターにも、モニター上で、ブロックを積み重ねていくようなプログラムが働いているらしい。
「コンピューターの構成の基礎知識」1と0の極限を目指す機械
それぞれ内部構成の違いか、ネットワーク関連の違いかはわからないが、ブロックの積み重なるテンポは違っている。
「ネットワークの仕組みの基礎知識」OSI参照モデル、IPアドレスとは何か
モニターaにブロックが1つの時、モニターbはブロックが2つ。
モニターaにブロックが2つの時は、モニターのブロックは4つ。
モニターaのブロック3つの時は、モニターbのブロック6つ。
ふたつの数の関係を示す代数式
別に難しく考えなくても、しばらく観察してたら、ブロックの数が増える速度に関して、ある関係が導けよう。
ようするに、「モニターbのブロックの数は、常にモニターaのブロックの数の倍。よってモニターbのブロック増加速度は、モニターaのブロック増加速度の倍」
代数学的には、両モニターブロックの数の関係は、モニターaのブロック数をA、モニターbのブロックの数をBとして、以下のように書ける。
上記のような、何らかの法則とか、変化具合とかを数式の形で表したものを『代数式』と言う。
言葉よりも簡潔に短く
別に、言葉で書いても、代数式で書いても、結論や言わんとしている事は同じである。
実際に、数学の祖は、 代数式なんてもの使わずに、なんでもかんでも、やたら言葉で説明したと考えられている。
代数学の父と呼ばれるディオファントスは、ピタゴラスよりも300年ほど後の人なのである。
「ピタゴラス数」求め方、見つけ方の公式。ピタゴラス方程式とは何か
しかし、まず、見比べてみればわかる。
明らかに、代数式の方が簡潔ですっきりしている。
「グレートブリテン及び北アイルランド共和国」では長いから、イギリスでOK。
「イギリス」グレートブリテン及び北アイルランド連合王国について
ある意味、代数式というのは、そのような思想の上にもあるのである。
簡単な話だが、「数式なら簡潔に書ける」という発想のもと、代数なんて学が誕生するまでには、ずいぶん時間（おそらく数世紀くらい）がかかっている。
『位取りの法則』と同じく、代数式というのは、今は当たり前すぎて あまり感謝されないが、実は、非常にありがたいものと言えるかもしれない。
「ゼロとは何か」位取りの記号、インド人の発見
現実を数で考えた時
モニター上で積み重なっていくブロックは、それを見ているあなたにとって現実である。
「意識とは何か」科学と哲学、無意識と世界の狭間で
数式（1）のような、両モニターのブロックA、Bの関係は、その変化を観察していれば得られる。
しかし、ある瞬間の状況しか知れないなら、 数式（1）がブロックA、Bの増加速度の関係を表すと、確信は出来ないだろう。
例えば「ブロックAが2の時にブロックBが4」の場合は、その増加速度の関係は、B=A+2かもしれない。
B=A^2の可能性もある。
あるいは、
ブロックAが0~3の場合（Bは、0、2、4、6）の情報が得られてるのだとしても、それなら、
「という関係であるかもしれない」と言われたら、おそらくは、「確かにそうだ」と返すしかない。
現実においては馬鹿げてるかもしれない。
この事はむしろ、数学を実用的に扱う上での、いったい数学的には許される事のどこからどこまで適用していいのかの、難しさを示しているように思う。
例えば物理学に数学が利用された時、答の中に（無限とか）違和感ある答が出てきたら、物理学者はそれを馬鹿馬鹿しいと切り捨てる事がある。
「特殊相対性理論と一般相対性理論」違いあう感覚で成り立つ宇宙
観測結果とかと、そんなに矛盾していないのに、「何かおかしくないか」、と不安になる事もある。
「量子論」波動で揺らぐ現実。プランクからシュレーディンガーへ
変数と関数。片方の変化に左右される片方
xがわかった時にyもわかる法則
2つのコンピューターの例における、ブロックAとブロックBの関連が、数式（1）ならば、必然的にAの値が決まった時に、Bの値も決定する事になる（もちろん、逆もしかりである）。
ある数xが決まったらyが決定するような場合、xを『変数』、yを『関数（function）』と言う。
そしてfという記号を使って、以下のような数式で表す。
この式（仮にf式）は、xの変化が、一定の決まりでyに作用する手順やルールがある事を表している。
数式（1）のx（A）がy（B）に与える作用は、「2倍する」という、簡単なものだが、もちろん、単に関数式のみ書かれている場合、xのyへの作用が、かなり複雑な計算を踏む場合はありうる。
f式は、とにかくある変数と関数が関連している事を、（ どういう関連なのかともかくとして）すぐさま知れるというのが、非常に便利である。
とりあえず「xがわかった時に、yもわかるような法則がある」という事を、この数式は示している。
「微積分とはどのような方法か？」瞬間を切り取る
一次方程式。一次関数は必ず直線グラフ
x = 1、2、3、4……
y = 12、14、16、18……
上記のx、yの関係は、以下のような代数式で表せれる。
このようなy = Mx + Cのような形の方程式を『一次方程式』。
そして一次方程式におけるx、yの関係を『一次関数』と言う。
一次方程式は、変化量がずっと変わらない。
ようするに、グラフに書くと、必ず直線の形になる。
のような形の式において、y、xの関係を『二次関数』。
のような式においては『三次関数』と言う。
これらは、一次関数の形から、容易に想像つくであろう。
n次方程式はすべて解けるか
二次方程式の解の公式
基本的に、
上記のような形の式は『一般二次方程式』と言うが、これは、解法が知られている、という意味で、非常に重要なものである。
一般二次方程式の形に直せばxについて解くための公式があるからである。
ようするにどんな計算式においても、上記の形にさえ出来れば、未知数xに関して解くことが可能なのだ。
一般に二次方程式は以下のように変形出来る。
上記を「二次方程式の解の公式」と言う。
例えば、一般二次方程式において、a、b、cがそれぞれ1、11、30だとすれば、解の公式にそれらをあてはめ、xが、5か6だという事を求められる。
解が2つあるが、通常、二次方程式には、解がふたつある。
二次方程式の解の公式のような、一般代数式は、ただ、それさえ知っていれば、同じ形で数字が異なる式を、解きやすいという、大きな利点がある。
代数学がいかに有益な思想であるかが、よくわかるだろう。
代数的に解ける式、解けない式
下記、
というような形の数式は、『一般三次方程式』と言い、これにも解の公式はあるが長い。
また、通常、三次方程式には解が3つあるとされる。
ようするにn次方程式には、解がn個あるらしい。
そして、その解は、代入する数に複素数を用いる場合、必ず複素数である事は、証明されている（この決まりは『代数学の基本定理』と呼ばれている）。
「複素数とは何か」虚数はどれほど実在してないか。実数は本当にリアルか
（その形は二次、三次を見れば容易に推測できるであろう）四次方程式は、やはりというか、解の公式はあるが、三次方程式よりさらに長い。
解の公式が発見されたn次方程式は、普通、「代数的に解ける式」と言われる。
かつては、（複雑な形にはなるだろうが）いかなる数nの次元の方程式も解けるだろうと、多くの人が期待していた。
実際には、四次方程式の解の公式の発見より、数世紀経ってから、「五次方程式以上には解の公式は存在しない」という事が、証明されてしまっている。
