「量子論」波動で揺らぐ現実。プランクからシュレーディンガーへ

量子という最小のひとつ

プランクの公式

　20世紀の最後の方。
多くの物理学者が取り込んだ問題に、『空洞放射（Cavity radiation）』のエネルギー分布というのがあった。
端的に言えば、これはある密閉空間内のエネルギーを、物理的な量として定めるにはどのような計算を用いればよいか？
という問題である。

　マックス・プランク（1858～1947）がこの問題に取りかかった時、真相に近いと思われる数式はふたつあった。
それは「レイリー・ジーンズの公式」と「ウィーンの公式」というもので、いずれも、成果はあるが、何もかも納得させてはくれない、という類いのものだった。

　どうやら、エネルギーは振動していると仮定して、一定時間内の、その振動数が低い時には、レイリー・ジーンズが、振動数が高い時にはウィーンが適用出来るようだった。

　そこでプランクはこれらの式を掛け合わせ、自らの式である「プランクの公式」を考え出す。
これは単純に、振動数が低い時には、式がレイリージーンズに近似になるように、高い時にはウィーンと近似になるような数式であった。
そしてこの公式は、非常に絶妙に、密閉空間内のエネルギー分布を上手く定量化した。

　プランクの公式

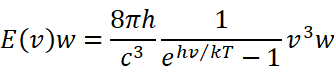
vとｗがある振動数、hがプランク定数、kはボルツマン定数、cは光速度

プランク定数

プランクの公式は、ある部分的に成功したふたつの式を混ぜるという、完全数学面からのアプローチによる産物であった。
だからプランクは、この式の成功に慢心せず、式の背後にある物理的な意味を求めた。
「物質構成の素粒子論」エネルギーと場、宇宙空間の簡単なイメージ
　なぜこの式は上手くいくのか？
エネルギーの図る基準が、まるでその振動数によって変化してしまうのはなぜなのか？

　プランクの結論は「エネルギーは非連続体である」というものだった。
物体が微小な粒子から出来ていると考えられているように、彼はエネルギーとは、微小な一単位の集合体なのだと考えたのである。
彼はそのエネルギーの最小単位を『量子（quantum）』と名付けた。

　プランクは量子が存在するのを前提として、自らの式から、重要な更なる結論を導きだした。
それはエネルギーは、必ず最小量hの整数倍であるという結論である。
このhという値は、今は『プランク定数（Planck’s constant）』と呼ばれている。

シミュレーションゲームのような

　エネルギーに最小単位があるというのは、どういう事を意味しているのだろうか？
実のところ、それが事実なら、我々という存在も案外奇妙になる。

　エネルギーは至るところにある。
適当にいくらか移動してみる時、そこには体を動かす運動エネルギーというものがかかっている。
仮に1mという距離を、最もエネルギーを節約した方法で移動するとして、その為に消費されるエネルギーをeとする。

　お気づきだろうか？
もしもeが、エネルギーの最小単位（つまりe=h）なら、我々は1m単位でしか移動が行えないという事になる。

　hが我々のスケールに比べて小さすぎるために実感できないが、エネルギーが連続的でないなら、それを使用する我々の動きも連続的であるはずがない。
モニターに移る、マス単位でしか移動出来ないシミュレーションゲームのキャラみたいなものだ。

　だが、ほんのわずかなエネルギーしか移動に必要ないミクロな領域では、この不連続的なリアルは、露になるであろう。
ミクロとマクロで、全く世界観が違うように思われる理由は、だいたいこの、実は不連続なリアルのせいである。
「ビットとは何か」情報量の原子は本質的にも原子であるのか「宇宙プログラム説」量子コンピュータのシミュレーションの可能性

光は波であり粒子でもある

　相対性理論で有名な、しかし当時は無名だったアルベルト・アインシュタイン（1879～1955）も、プランク定数という衝撃に影響を受けたひとりだった。
「アインシュタイン」人類への功績、どんな人だったか、物理学の最大の発明家「特殊相対性理論と一般相対性理論」違いあう感覚で成り立つ宇宙
　光が波であるか、粒子であるかの議論は古くからあり、アインシュタインの時代には波説が、有力であった。
しかしアインシュタインは光を金属などに当てた時に、電子が放出される『光電効果（Photoelectric effect）』という現象が、光が粒子でないと説明出来ない事を示したのである。

　アインシュタインは光が波ではない、と言ったのではない。
彼は光が、粒子の性質も持つのだと言ったのである。

　つまり光は、波でありながら、粒子でもあるわけである。

　その説は『光量子仮説（Light quantum hypothesis）』と名付けれ、後にはその光の粒子は『光子（photon）』と呼ばれるようになった。

原子構造。二つのモデル

原子の内部

　これも20世紀の終わり頃。
『放射線（radiation）』を出しながら崩壊したりするという現象より、それまで物質の最小の構成要素だと考えられてきた『原子（atom）』に内部構造があるのではないか？
という疑いが出てきた。

　密閉空間内に電圧をかけると、内部（の気体（？））に放電現象が起こるから、原子の内部には『電子（Electron）』がある事も示唆されていた。
「電磁気学」最初の場の理論。電気と磁気の関係
　放射線や放電現象などの研究により、原子内部を構成しているのは、マイナスの『電荷（electric charge）』を持つ電子と、プラスの電荷を持つ何らかの成分である事もわかってくる。
そして最も軽い原子である水素（H）に比べても、電子はかなり軽いから、プラス電荷を持つ何かは、電子よりかなり重たいであろう事も予想できた。
「中間子理論とクォークの発見」素粒子物理学への道
　そして1904年、ジョゼフ・ジョン・トムソン（1856～1940）が『プラムプディングモデル（plum pudding model）』を、長岡半太郎（ながおかはんたろう）（1865～1950）が『土星型モデル（Saturn model）』と呼ばれる原子の内部構造モデルを発表したのだった。

α粒子の経路

　プラムプディングモデルは、球場に広がるプラスの電荷が、内部に電子を閉じ込めているという原子構造モデル。
一方で土星型モデルは、プラス電荷を持つ何かが中心にあり、その周囲を太陽系の惑星のように、電子が回っているという原子構造モデルである。
「太陽と太陽系の惑星」特徴。現象。地球との関わり。生命体の可能性
　正しい原子構造モデルを見極める為に、ハンス・ガイガー（1882～1945）とアーネスト・マースデン(1889～1970) は1909年にある種の実験をかなり詳しく行った。

　α粒子はプラスの電荷を持ち、質量はほぼヘリウム（He）原子に等しい粒子である。
このα粒子がヘリウム原子をすり抜ける場合、内部のプラス電荷成分と、電子との間の電磁気学的な作用を受ける。
するともちろんα線（α粒子の進む経路）は曲げられるはず。
しかも、α粒子は電子よりもかなり重たいから、影響はほぼプラス電荷によるものと考えられる。

　もしもプラス電荷成分が原子内で均等なプラムプディングモデルが正しいなら、α線への影響はあまりない事は、トムソン自身が計算で示していた。
一方で、プラス電荷成分が、原子の中心に固まっている土星型モデルなら、α線は原子の中心付近で、特に大きく曲げられるはず。

　実験結果は、α線はたいていの場合、あまり影響を受けない。
しかし時々、急激に屈曲されるというものだった。

原子核の発見

　多くの人が、正しいのはプラムプディングモデルであると考えた。
α線が時々急激に曲がるのは、単に均等に分布したプラス電荷成分の小さな影響が、積み重なったにすぎないと。

　だがアーネスト・ラザフォード（1871～1937）は違った。
彼は確率論的な計算により、プラムプディングモデルを前提とした場合、時々の大きな屈曲の頻度が高すぎる事を示したのである。

　1911年。
ラザフォードはさらに実験結果と計算結果を照らし合わせ、原子のプラス電荷成分は、原子内部中心に核として集中している事。
さらにその、『原子核（nucleus）』の電荷量に関する貴重な情報まで明らかにした。

　電気素量（電子一個と中性になるプラス電荷の量）をeとする。
そして原子核の電荷をZeとすると、Zは実験に使う原子の原子量（炭素原子の質量を12として決められた、原子の相対的な質量）の半分に（わずかな誤差はあったが）等しい数だと示したのだ。

　後にアントニウス・ブレック（1870～1926)は、ラザフォードが示した原子核の電荷ZeのZは、実は『原子番号（Atomic number）』と同じである事に気づいた。

　こうして原子内部の中心には、原子番号×eのプラス電荷を持つ重たい原子核がある事。
基本的に中性の原子内部には、原子核のプラス電荷を打ち消す為に、やはり原子番号と同じ数の電子が存在している事が明らかとなったのである。

土星型の問題点

　ラザフォードが導きだした結論は、明らかに土星型モデルを支持している。
だが、土星型モデルには重要な問題があった。

　原子核がプラス電荷、電子がマイナス電荷なら、電磁気学の法則により、このふたつの成分は互いに引き合うはずである。
つまりくっついてなければおかしい。
それを回避するには、電子は常に動き、その遠心力で原子核からの引力に逆らうしかない。
太陽の引力に逆らって、回りを巡る惑星のように。

　だが密閉空間内での放電現象は、原子から電子が放出される事がある事を示している。
電子が原子核に落ちていかないのは、引力と遠心力が上手く釣り合った場合だけであるが、そうそういつも、原子内に入った電子は、上手い事回るだろうか？

　そもそも、電子のような荷電粒子が動く時には、光（電磁波）が射出するはずである事は、ジェームズ・クラーク・マクスウェル（1831～1879）が示していた。
「マクスウェル」電磁気学の方程式、土星の輪、色彩、口下手な大物理学者の人生
　それはつまり、電子が原子核の周りを巡るなら、電子はだんだん（光が持っていく）エネルギーを失っていくはずである事を意味している。
いつまでも定位置を維持しておく事など出来るはずないのだ。

エネルギー定常状態

　ここで土星型モデルの問題点を、プランクが考えた量子という概念を使えば解決できるのではないかと、あなたは考えたかもしれない。
ニールス・ボーア（1885～1962）はそう考えた。

　ボーアはラザフォードの理論に、プランク定数hを突っ込んで見たのである。

　つまり、原子のエネルギー状態は不連続で、その値がある段階で止まった時、最小エネルギー単位を飛び越すほどの影響がなければ光は放出されない。
移動が1mずつしか無理なのだとして、50cm動かすくらいの力では動かない、みたいな感じである。

　またエネルギーが不連続である事の影響は、電子や原子核のスケールでは大きいとすれば、（引力と遠心力の）エネルギーが釣り合うのも容易いであろう。
電子の空間的な位置すら、はっきり不連続であるかもしれない。

　ボーアは、原子があるエネルギーで安定してる時を、定常状態として、原子が光の射出や吸収を行うという事は、すなわちある定常状態から、別の定常状態への切り替わりだと結論した。

電子殻

　ボーアのアイデアは非常に上手くいき、いくつか重要な副産物もあった。
『電子殻（Electron shell）』の概念などまさにそれであろう。

　電子殻は、原子核を巡る電子の軌道であり、電子のエネルギー量を基準とした階層を成していると考えられている。
階層は、エネルギー準位の低い方からK殻・L殻・M殻・N殻・O殻・P殻と連なり、各殻には定員が定められている。
例えばK殻には2、L殻には8までの電子しか入らないようなのである。
この事実は原子番号の限界も示唆している。

　しかしながら、ボーアのアイデアは、決して完璧ではなさそうだった。
というのも、彼の考えを前提とした計算でも、その構造に関して綺麗に説明出来た原子は、核と電子が1個ずつという、単純な水素くらいだったのである。

波動に例えられるのは、本当は何なのか

スピン

　体を回転させると、周囲が見える。
だが電子のスケールではどうか？

　ボーアのアイデアが上手くいくように考える過程で、電子の軌道運動による角運動量（円運動の大きさを示す量）の力が働く方向すらも不連続である可能性が出てくる。
それは『方向量子化（Direction quantization）』と呼ばれた。

　また、ヴォルフガング・パウリ（1900～1958）は（エネルギー量や方向の）同じ量子は2つまでしか存在出来ないと示した。
彼の考えは『パウリの排他原理（Pauli exclusion principle）』と呼ばれていて、もちろん電子殻のアイデアと関連が深い。
しかし2つまでとはどういう事か？

　それはこういうわけだった。
ジョージ・ウーレンベック（1900～1988）とサミュエル・ゴーズミット（1902～1978）は、電子自体が固有の角運動量を持っているとするなら、当時矛盾とされていたいくつかの実験結果を説明出来ると発表したのである。
あろう事か、彼らはその角運動量は電子の自転『スピン（spin）』に由来しているとしたが、現在では、あまり自転とはされない。

　スピンが自転にしろ、何にしろ、ふたつの（自転だとしたら方向）パターンを持つ。
これはパウリの排他原理より後の発見だから、パウリは同じ状態の量子は2つまでとしたのである。
本当は1つまでだったわけだ。

　排他原理もスピンも1925年の発表であった。

物質も量子から成る

　1923年。
ルイ・ド・ブロイ（1892～1987）は、ボーアのアイデアに、光の波であり粒子でもあるという性質を取り入れた。

　彼は電子のような物質を構成する粒子も、実は量子というべきもの。
つまりは、光子のように、波の性質も持つ粒子なのだと考えたのだ。
そして、原子内部を考える過程で、次々に明らかとなってきた不連続性は、電子などの波の性質の干渉によるものなのではないかと提唱したのである。

　ド・ブロイの発表はあまり注目されなかったが、幸いにも、彼の考えに注目した少数派の中にエルヴィン・シュレーディンガー（1887～1961）がいた。
彼は、ド・ブロイのアイデアを前提に、電子などの波の性質を示す方程式を1925年に発表したのだった。

　シュレーディンガー方程式

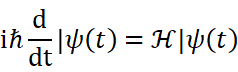
iが虚数、dが時間で、Hがディラック定数（h/2π）、ψが波の関数。

不確定性原理

　ヴェルナー・ハイゼンベルク（1901～1976）はシュレーディンガーとは全く違うアプローチで、しかし、同じような（あるいは同じ）答にたどり着いた。

　粒子の波動性に注目したド・ブロイと違って、ハイゼンベルクは、粒子の空間的な配置や運動量そのものにメスを入れた。

　人は何かの情報をどうやって入手するのか。
人でなくとも、あらゆる物は、その他の万物と干渉するにはどうすればよいのか？
見る、聞く、感じる、その全てエネルギーの伝達である。

　しかし大きなエネルギーで小さな物を見る事は出来ない。
人を見た時、原子の集まりのはずなのに、原子が見える事はない。
ならエネルギーを小さな範囲に絞るのはどうか？
しかしそうすると、集中して高まったエネルギーは、干渉対象を弾き飛ばしてしまう。

　そういう原理で、この世界の最小スケールの物の位置と状態を、同時に知る事は決して出来ない。
これは『不確定性原理（Uncertainty principle）』と呼ばれている。

　計算上は、粒子の波動性と同じ結果になる場合も多いが、両者は組み合わせて考えられる事もあるが、別物として扱われる事も多い。
実際、真実に近いのは波動性の方だと考える人が多い。

確率解釈

　しかし粒子の波動性とは何なのか。
1926年。
マックス・ボルン（1882～1970）は、粒子の波動について、それは確率であると示した。

　例えば、箱の中に電子が一個だけ入ってるとする。
電子が最小の構成要素だとしたら、それ以上分割出来るわけがない。

　だが電子は波でもあるならどうか？
箱の内部に広がる、電子の波を仕切りで切り離したら、どうなるか？
別れるはずのない電子は別れるのだろうか？
それともその瞬間に波の性質は消え去り、仕切られたどちら側かに、粒子としての電子が現れるのだろうか？

　ボルンは後者の立場で、かつ、仕切りによって消された波は、仕切りのどちら側かのあらゆる所に電子が存在した確率の波だと考えたのである。

　物質（粒子）は波の性質も持つ。
そしてその波とは確率の波。
それが量子論が導きだした、一般的な答であった。

いずれにしても確信している人たち

　物質を構成する粒子、そしておそらくはその粒子の集合体である物質は、確率の波を放ち、別の何かと干渉しあう時にだけ、確率のひとつが現れる。
こんな世界観は理解しにくいが、そう考えるのが最も矛盾が発生しないのもまた事実である。

　この世界の曖昧さ加減は間違ってるという人は多い。

　アインシュタインは生涯、量子論の確率解釈はおかしいと信じ続けた。

　いつか、彼は言ったという。
「じゃあ、あの月があそこにあるのは。誰かが見てるからなのか？　誰も見てないなら、あの月は単なる確率なのか？」

　いずれにしても（例えどれだけ量子論の正しさが示されても）実は多くの人が確信している。
神はサイコロをふらないと。

量子論とあまり関係ない話

　2000年以上前の古代ギリシャの哲学者たちは、「世界は数字で出来ている」と言った。
これは実にわかりやすい勘違いである可能性は高い。

　一方、難しい量子論というもの、あるいはそれに関連したあらゆる物理学理論を、わかりやすく説明するには「例えがいい」と現代の物理学者たちは言う。
これはどう考えても誤解を招きかねない表現である。

なぜ数字が重要なのか？

　世界を理解するのに数字が便利である事は間違いない。
例えばあなたが友人に「私（あなた）の特長って何だと思う？」と聞いたとする。
友人が、あなたに関するあらゆる数字（身長、体重、座高、心臓の振動速度の平均とか）を述べたならどうだろう。
そこで「気持ち悪い」と思わずに、よく考えると、友人はあなたの事を確かに理解しているようではないか。

　あなたと友人が恋仲になって手を繋いだとしても、あなたと会った事もないが（なぜかはともかく）あなたの手に関する数字（指の長さとか、通ってる血管の数とか）をたくさん知ってる第三者の方が、恋人よりもあなたの手に関して詳しいと言える。
人はなぜ恋をするのか？「恋愛の心理学」
　文字というのはあまり当てにならない。
例えば地球だ。
今、あなたはこの足をつけた星を地球と呼んでるだろうが、アメリカ人はそう呼ばない、インド人もアゼルバイジャン人もそう呼ばないだろう。
もちろんアステカ人もメソポタミア人もそうは呼ばなかったろう。
「アステカ文明」帝国の首都、生贄文化、建国神話、社会の階層シュメール、アッシリア、バビロニア「メソポタミアの古代文明」
　だが10進法で、何らかの現象を記述する場合、例え数字の呼び名が違う、日本人とアメリカ人でも、最終的には同じ理解にたどり着くだろう。

　人間が使う基準で数字ほど、一般性の高いものはない。
そういう意味では数字は、理解するのに便利というより、伝えていくのに便利と言える。

なぜ例えが便利なのか？

　数学がそもそも簡潔な例えみたいなものだ。
用法が難しいから、難しいと言われるだけ。

　1000匹の犬が檻の中にいるとする。
その内のほとんどが逃げてしまって、後で檻に残ってたのは3匹だけだったとする。
逃げ出した犬の数を知るのに、あなたが引き算というものを知らなければ、逃げた犬を全部捕まえて数えるしかない。
「数字と数式の種類」数学の基礎の基礎。
「なんてめんどくさい。もっと楽な方法はないのか？」
あなたは思うに違いない。
多分、誰かが引き算を教えてくれたら、あなたはその人を英雄と呼ぶ事だろう。

　だから物理とか社会とか、複雑な事を考える人は数学が好きなのである。
複雑な事を簡潔にしてくれるからだ。

　だが数学はそれ自体がなかなか複雑な機構であり、理解するのが難しい。
そこで物理学者はもっと簡単な例えを使う。
数学ほどに簡潔には出来ないが、簡単で理解しやすいからだ。

　ここで言いたいのは、物理学者が説明するのは、いや理解している量子論関連の全ては、例えにすぎないという事。
「例えが便利」とはかっこつけた言い方である。
真実は「物理学者すら、例えしか知らない」である。

誰にも理解出来ないのは当たり前

　量子論ではないけど一般相対性理論を例に上げる。

　あれによると、重力の正体は時空間の歪みであるらしい。
世界を幾何学的な（時間を含めてない）3次元空間と仮定し、そこに置かれた物質の質量に応じて、各物質が進む（空間的な）経路を曲げると考える。
すると少なくとも、数学的には、重力に関する諸現象の多くを説明できる。
「ホログラフィック原理」わかりやすく奇妙な宇宙理論
　だが、一般相対性理解的な重力の理解は、トランプの手品が裏に書かれてた目立たないマークだと見破るような理解とはまるで違っている。

　簡単な事。
量子論によると、世界のもの、例えばある人という存在は微小な粒子の集合体らしい。
しかし仮に、あなたが驚くべきほどの計算能力を持って、ある瞬間のあなたの友達を構成する全ての粒子の数や動きを把握したとする。
多分あなたは、その瞬間の友達という存在の全てを知ったと言える。
でもあなたがどれだけ目をこらしても、その瞬間に認識出来るのは、ただひとりの誰か。
それだけである。

　理解が難しいのは当たり前だ。
本当に何が起こっているのかを誰も知らないのだから。
ただその起こってる事を、ある数学体系の動きに例えたら、ある程度ぴたりとハマっているだけなのである。