黄金比。黄金数。もっとも美しい比率
線abの途中に点cをとって2つに分割する時。
ab : bc = bc : ac
が成り立つような比a : bの事。
これが何かと言うと、最も美しい比率らしい。
この比率通りに作られたものは、とても美しいと、多くの人が感じるのである。
例えば2色の色だけを使った柄を作る場合に、どこで色を変えたらいいかなどを、この比率を基に作ると、美しいものが出来上がるのだという。
ピラミッドのような古代の建築物にも、この比率を適用して作られたものは多いとされる。
正確な黄金比（golden ratio）は、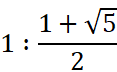
である。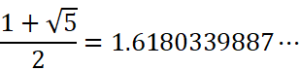
はまた、x^2 − x − 1 = 0という方程式の解のひとつであり、黄金数（golden number）と呼ばれる。
ユダヤの法則。恋愛、投資、あらゆる分野にて成功する為の比率
これは黄金比率よりも、かなりオカルトじみた比率。
とりあえず合計100の中で、78対22らしい。
ユダヤ人が開発したからユダヤ比率と呼ばれるのかすら謎。
「ユダヤ教」旧約聖書とは何か？神とは何か？
よく言われるのが、人間の体を構成する素材が、水分78に対し、その他の物質が22。
大気の成分の割合は、窒素が78に対して、残りの成分が22。
地球の海の面積78に対し、陸地面積の割合が22。
さらに、円に外接する正方形の面積を100とすると、円の面積は78、残りは約22となるらしい。
そして、金を貸したい人78に対して金を借りたい人は22人。
あるいは、お金持ち78に対し貧乏人12だという。
なんか恋愛や投資にこの比率を利用したら上手くいくらしい。
人はなぜ恋をするのか？「恋愛の心理学」
ある意味一番衝撃的なのは、これに関して、まるで一切疑っていないかのような紹介をする人が、結構いることである。
正直、大気の成分や、地球の海と陸の面積の話などは、かなりバカバカしいものにしか思えないのだが。
「雲と雨の仕組み」それはどこから来てるのか？
「プレートテクトニクス」大陸移動説からの変化。地質学者たちの理解の方法
フィボナッチ数列。黄金比との関係
1、1、2、3、5、8、13、21、34、55、89……。
というような数列。
このフィボナッチ数列（Fibonacci sequence）は、どの一項をとっても、必ず前の二つの項の和になる。
このフィボナッチ数列は、自然界に多くあると言われる。
特に有名なのが、ひまわりの種。
ひまわりの花は、種が螺旋上に並んでいるが、それを数列にするとフィボナッチ数列が現れるのだという。
また、フィボナッチ数列の、隣り合うふたつの数の比は、
2 : 3 ＝ 1 : 1.5
3 : 5 ≒ 1 : 1.666666
5 : 8 ＝ 1 : 1.6
8 : 13 ＝ 1 : 1.625
13 : 21 ＝ 1 : 1.61538
というような感じで、黄金比に近づいていくと言われる。
名数とは
同類とされるものをいくつか集め、まとめて表したものを名数（めいすう）という。
三大〜とか、四大〜とかいうやつである。
御三家、三馬鹿、三人娘、三種の神器など、 なぜか3がよく好まれる傾向にあるようである。
「天皇家の雑学」宮家とか、三種の神器とか
例えば、三代集と言うと、平安時代の三つの勅撰和歌集の事。
勅撰和歌集（ちょくせんわかしゅう）とは、天皇や上皇の命により編集された歌集。
三代は、古今和歌集（こきんわかしゅう）、後撰和歌集（ごせんわかしゅう）、遺和歌集（しゅういわかしゅう）
ややこしい事に、 漢字が違って三大集だと、万葉集、新古今和歌集、古今和歌集になるという。
3はめでたい数字とされる事もあるが、不吉な数字という話もある。
それが、「散々」に通じる響きだかららしい。
さん3の不吉な話は、例えば3人で写真を撮ると真ん中の人が早死にするとか、そういうのがある。
1ドルが360円だったのはなぜか
今は外国為替のレートは変化するものだ。
しかし、1970年代ぐらいまでは固定金額であったという。
1ドルは必ず360円だったのである。
これは日米の偉い人達が取り決めたことらしいが、決めたのはアメリカ人の方だったとされている。
どうも、なかなか話がまとまらず、ピリピリした空気の中で、一人のアメリカ人が言ったらしい。
「円ってのは丸のことなんだろう。丸い円は360°だから、もう1ドルは360円てことにしよう、それでいいじゃないか」
数字が無限に続くとなぜわかるか
数字は無限にあると言われる。
だがなぜ誰も、全てを数えたことがないだろうに、無限とわかるのか。
簡単な話である。
例えば仮に、lastという数が最後の数字だったとしよう。
そしてその数字まで数えた人がいたとする。
その人に、誰かが言った。
「じゃもうひとつ、lastの次はnewにしよう」
これでもうlastは最後の数字ではなくなった。
1+1=2はなぜなのか
たいていの人が知ってる、単純なこの数式は、しかしなぜこのような結果が出るのか、考える人が少ない。
「数字と数式の種類」数学の基礎の基礎。
この式は、古代ギリシャではおそらく、
「数直線上で。1から右に1目盛り進んだ場合、どの数になっているか」
という問題であった。
もっと言うなら、ギリシャ数字は、後にインドにて開発されるアラビア数字とは違うので、1+1という数式の答に関して、認識が違う。
例えば2なら、最も基本的な数である1を示す記号をふたつ並べた数だったのだ。
つまり
1+1 = 2
は
1+1 = 1+1
だったのだ。
つまり、=の前後が同じ数だったから、そもそもこれは考えるまでもないことだったのだ。
1はなんで1か、というような問いに近かった訳である。
ちなみに19世紀以降は、自然数は集合論で定義されることが普通である。
つまり1+1は1という数を元とする集合ふたつの和集合と考える。
なぜ集合論なのかというと、実は、1+1 = 2というのが、明確に証明されたのは、ようやく19世紀のことであって、それを証明するのに使われた数学理論が集合論だったのである。
また、ゲーデルという人が、集合論を基準として算術を考えた場合、導かれた算術のルールが、必ず無矛盾であることは証明できない、ということを証明している。
つまり、1+1 = 2というのが確実な事だとは、少なくとも現代の知見では言えない。
別におかしな話でもなんでもなく、1+1 = 3かもしれないのだ。
