ある量より小さな素数はいくつあるか？
素数とはその「その数以下の数では、その数と1以外で割りきれない数である」。
例えば11/n（11÷n）を考えてみる。
nに1、2、3……11までの数を代入していって、答に余りがでなかったのは？
あなたがどこか、知られざる世界に生きている訳でないなら、答は1、11だけだったに違いない。
そういう（11）みたいな数字が『素数（Prime numbers）』と呼ばれるものである。
10より小さな素数は何個あるか？
これは実に簡単な問題。
答は4つ（2、3、5、7）
しかし10000までの素数の数は何個あるか？
という問題を簡単だという人はあまりいないと思う。
ただしこの問題も、コンピューターの使用が許されるなら簡単な類に入るだろう。
だがそれも1グーグルプレックスプレックス（0が多すぎてひとりの一生使っても余裕で書けないくらいのレベルの数）までの素数の数となると、どうか？
「与えられた量より小さな素数はいくつあるか？」
この問題に（正攻法で数えていく以外に）答を出せる、法則や公式のようなものがあるとしても、1グーグルプレックスプレックスの場合の答については誰も出せないかもしれない。
（出したとして、その答の数を上手く表現出来ないと思う）
しかし1000000までの素数とかなら、その方法で、アナログ人間の数学嫌いでも出せるようになるかもしれない。
かつて、ドイツの数学者、ゲオルク・フリードリヒ・ベルンハルト・リーマン（1826～1866）は、この問題に取り組んだものの、結局、途中放棄したという。
彼自身が論文で述べているように、この問題は多分、彼の「研究には直接関係ない」問題だったから。
「第五公準、平行線問題とは何だったのか」なぜ証明出来なかったのか
単なる言い訳かどうかは、今では神のみぞ知る。
無限への道、有限値への道
級数
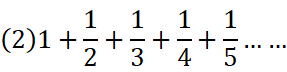
数式（1）は、「1から続く自然数」を順に（無限にあるそれら）全てをひたすら足していくという式。
数式（2）は、「1/n」をひたすらに足していく、ただしnには「1から続く自然数」を順に代入していくという式。
というような何らかの決まりに従った無限に続く数をひたすらに足していく数式を『級数（series）』と言う。
Σを使った記法はわかりやすい。
例えば、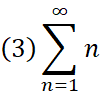
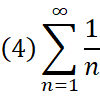
というように書く。
「数列の基礎」和の公式。極限と無限。単純な増加、減少
「数を数えること」自然数とは何か。その時、我々は何をしているのか
極限への発散と収束
一般的に数式（1）も（2）も答は∞になる。
「級数が無限になる」とは、その級数メートルの道が無限に続いてく事を意味する。
つまり（1）メートルも（2）メートルも∞メートルに延び続けるのである。
このように級数の答が無限に大きくなっていく事を『発散（divergence）』すると言う。
一方で、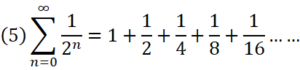
のような級数は発散しない。
実は（5）メートルの道は、決して2mに届かない。
（5）の級数の無限に続く計算をどこで止めて答を出しても、それは2より小さな数になる。
そこには確かに無限があるが、その無限の道の到達地点は、無限の果てでなく2なのである。
このような場合、（5）のような級数は2に『収束（convergence）』する言う。
そして発散や収束する到達てんの数を『極限（limit）』と言う。
例えば（5）は「2の極限」という訳である。
それを多分、知ってる
無限に続く数なのか？
そうである事は、既にユークリッドが書いた、紀元前の数学書である『原論（Elements）』の中でも証明されている。
ユークリッドの証明とは以下のようなものだ。
まず前提として、ある数xと1以外の、ある数xの最小の約数は『真の約数』と言い、必ず素数である。
（つまり素数とは真の約数がない数である）
基本的な演算のルール上、xの約数yにも真の約数zがあるなら、そのzはまたxの約数にもなる。
パンケーキを正確に3つに分けたとして、分けられたそれぞれをさらに2つずつに分けたとして、それは元のパンケーキの6等分というだけの事、みたいなものである。
Nを素数として、「1×2×3×……×N+1」という数xの約数について考える。
xが素数なら、それがNよりは大きいのは明らかである。
xが素数でないとしても、その最小の約数yは、（N以下の数では1余る為に）、N以上になるはず。
そのxの最小の約数の数yが、素数でないならば、（xはyの約数でも割れるはずなので）yは最小の約数でなくなる。
つまりyは素数であり、Nよりは大きくなる。
という考えは、どのような素数Nを使っても適用出来るから、どんな素数にも、さらに大きな素数が存在する事になる。
素数に法則性はあるか？
素数が無限に続く。
それは間違いない。
しかしそこに、つまり素数の続きかたとかに、規則性があるのかどうか？
これこそがリーマンの問いだった。
「10までの数に、素数は4個」、「100までの数に、素数は25個」
というと、いかにもそこに何らかの法則性を期待出来る。
例えば100/25=4と、実に意味深に思える。
しかし「1000までの数に素数は168個」と知ってしまうと、がっかり感が出てくる。
仮に何らかの法則があるとしても、それはかなり複雑で見つけにくいに違いない。
eとInと、円周率でないπ
『ネイピア数（Napier’s constant）』という数がある。
ふつうは「e」という記号で表される。
e = 2.718281828459045235360287471352……と無限に続いていくこの数は、オイラー（1707～1783）によると、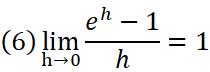
を満たすような場合の数eとされる。
limとはある数（式（6）の場合h）を、ある数（式（6）の場合0）へとひたすらに近づけていく、という事を表す記号。
「オイラーの生涯」研究と計算ばかりの伝記。家庭的で、ユーモアがあって
In、あるいはlogという記号もあり、これは「In y」などと書いた場合に、「y=e^x」になるような数xである。
例えばIn 2ならばx=0.69314718056（2=e^x）、In 5ならばx=1.609437912434（5=e^5）という事になる。
ただ、log xは「10^x」を表す場合もあるので注意。
「微分積分の関係」なぜ逆か。基本公式いくつか。指数対数関数とネイピア数
また、例えばx=yの場合、x=2ならば、y=2になろう。
2x=yの場合は、x=2の時に、y=4となるはず。
そういう場合にある数xを『引数（argument）』、あるいは『変数（variable）』と言い、引数によって決定する数yを『関数（function）』と言う。
引数x以下の数に「素数の個数」という関数yがどれだけあるかを表す関数の式は「π(x)=y」と書くのが普通。
このような関数式を『素数計数関数（Prime-counting function）』と言うが、式のπは、円周率のπとは何の関係もない事に注意である。
もしかしたらかなり近い
さて、注目すべきは「N/π(N)=x」という関数式である。
この式の引数Nが10ならば、関数xは2.5。
Nが1000ならば、xは5.9524。
Nが1000000ならば、xは12.7392である。
それがどうしたと思うかもしれないが、
In 10=2.302585092994。
In 1000=6.907755278982。
In 1000000=13.815510557964。
という事を知れば（あるいはさらに大きな数の代入で試せば試すほどに）、InとN/π(N)という関数には関連があるのではないか、と思えてこよう。
つまり「In N～N/π(N)」という訳である。
～は、「近似できる」「かなり近しいだろう」「もしかしたら実は同じ」という事を表す記号であり、In～N/π(N)のような一般式では、「=」と近い使い方が出来るのが普通。
つまり「y=x/2x」のような式を「2x=x/y」にしたり、「100=100/1」のような式を「1=100/100」として問題ないように、In N～N/π(N)を「π(N)～N/ln N」と変換出来る。
無限なる素数
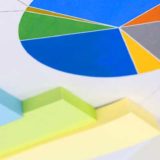
ゼータ関数
「n^x」はnをx回掛けた数となる。
では「n^-x」はどうか？
『巾乗（exponentiate）』の計算において、n^xを減らすのは、nを掛ける回数を減らしていくのと同じ。
掛ける数を減らしていくとは、割っていく、つまり1/aを掛けていくのと同じ。
するとn^0の巾乗は1。
n^-1は1/n。
n^-2は1/2n。
つまりn^-xは1/xという事になる。
として、ゼータ関数とは何か？
これはつまり、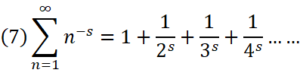
を満たすような数sの事であり、ζという記号を使い、「ζ(s)」と表記されたりする。
ゼータ関数のsが1という事はない。
どういう事かと言うと、ゼータ関数のsが1なら、それは無限に発散してしまう級数（2）と全く同じものになるからである。
無限という数は存在しないと思われるので、1が0の場合は、ゼータ関数という存在も消え去る。
当たり前の話だが、ホットケーキに卵と牛乳が必要なら、この世界から卵か牛乳が全部消えさってしまった時、それはホットケーキの消失をも意味するみたいなものである。
微積分と対数積分関数
微分というのは、もともと時間を変数として、ある物体の空間的な位置を関数と考え、その瞬間（ある時間）を考察する事によって導き出せる新たな『導関数（derived function）』、例えば物体の正確な速度とかを知る為に考え出されたもの。
積分は、円などの、面積を計りづらい図形の面積をなんとか計れないかという挑戦から生まれた、様々な面積を知る方法である。
微分は、グラフに書いた何らかの関数の、瞬間の傾き具合を知る方法でもある。
例えばx^2を微分すると、2xとなる。
これはy=x^2という式のグラフのメモリがx=nの時におけるyのグラフの上り具合（あるいは下がり具合）がnxである事を意味している。
積分は微分の逆の手順の計算をする。
例えばグラフの傾き具合から、あるメモリの時の数値を導き出せる。
例えばx^-1を積分すると、In xとなる。
また例えば、∫という記号を使って、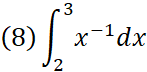
などと書いた場合は、つまり「x^-1について、2から3まで積分する」という事を意味する。
これはxが2の時のグラフ位置Xから、xが3の時のグラフ位置Yまでの面積を出すに等しいのだが、その場合、Y-Xをすればよい。
（8）はその事を端的に表す表記法である。
そういう訳で、例えば1/In tという関数を0からxまで積分するならば、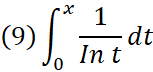
という事になる。
この（9）は『対数積分関数（logarithmic integral function）』と呼ばれ、「Li(x)」と表記される。
Li(x)=（9）な訳である。
素数定理
実は（9）がLi(x)などという専用の表記方が与えられているのは、「Li(N)～N/ln N」だからと言ってもいい。
つまり「π(N)～N/ln N～Li(N)」でもあるので、「π(N)～Li(N)」でもある。
π(N)～Li(N)、あるいはπ(N)～N/ln Nは、『素数定理（Prime number theorem）』と呼ばれている。
エラトステネスのふるい
紀元前230年頃くらい。
つまりリーマンよりも2000年くらい前。
アレクサンドリア図書館の司書だったらしいエラトステネスという人が、後のリーマンと同じ疑問を抱いた。
つまり、ある数以下の領域に素数がどれくらいかを数えるのに、何かよい方法はないものかと。
そして、彼が最終的に考えついた方法は以下のようなものだった。
とりあえずNまでの素数を数えるとして、その数字を全部紙に書く。
2はそのままに、その倍数を全部消す。
なぜならそれらは2で割れるから素数ではありえない。
これで2を除く偶数は全て消えた。
次に3をそのままに、3の倍数を全て消す。
次は5、その次は7。
という風に続けていけば、やがて紙面で消されていない数は全て素数となる。
このふるいわけ法を『エラトステネスのふるい（Sieve of Eratosthenes）』と言う。
黄金の鍵
エラトステネスのふるいと似たような発想を持って、例によってオイラーは、ある重要かもしれない事実を導いている。
ゼータ関数に1は発散するからないと書いたが、結局式（1）となる0もない。
実際その通りみたいだが、1以下で0以上の数は全てゼータ関数として存在できない事は容易に予測出来る。
ただとりあえず1より大きい数なら何らかの数には収束するという。
そこで、sが1より大きい場合のゼータ関数ζ(s)について考える。
まずゼータ関数を1/2^s倍する。
するとこうなる。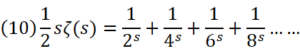
そしてζ(s)から、（10）を引き算する。
とこうなるであろう。
つまり分母が偶数の数が全て消え去る。
次は（11）を1/3倍して、出てきたのを、（11）から引く。
（11）の左辺は「(1-1/3^s)(1-1/2^s)ζ(s)」という風になって、右辺からは、分母から3の倍数が全て消える。
というのをエラトステネスのふるいのように、5、7と繰り返していく。
これをひたすらに続けていくと、分数は消えていき、やが（11）の右辺の数は1に収束するであろう。
そして左辺の（1-1/x^s）のxは全て素数となるはず。
その全ての（1-1/x^s）で、順次両辺を割っていくと、
となる。
（12）はゼータ関数sに関して、（素数をpとして）1-(p^-s)^-1をひたすら掛けていくというのに等しい。
ひたすら足し算していくのを表すにはΣを使うが、（12）のようにかけ算していく場合はΠを使う。
そしてゼータ関数もΣ記号で表現し、（12）は簡単に、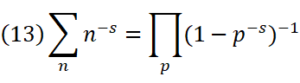
とも書ける。
この両辺は共に無限に続くので、これはまた、素数に限界がない事も示している。
リーマン予想
虚数、複素数、複素平面
生物分類学の階級を数字に適用して考えるなら、『複素数（complex number）』は、もっとも広く数字を含む、最上級の階層になると思われる。
-1の平方根、つまり2乗すると-2になる数を『虚数（imaginary number）』と言い、記号iで表す。
複素数とは、iを用いた計算から出た数であり、これはあらゆる数全てである。
例えば5は「5+0i」という風に書ける。
複素数は実数の世界にはないようにも思われる。
しかし少なくとも、実数と同じように、複素数を平面のある位置の点として、考える事が出来る。
そのように想定される複素数の領域を『複素平面（complex plane）』と言う。
また、複素数は実数を含む数なので、完全に実数と別世界にある訳ではない。
複素数の実数面にある軸点を『実部（real part ）』と言う。
自明の零点
複素平面上において、ゼータ関数をより深く定義していくと、結果的に負の偶数、全てが0に収束する。
つまりζ(x)=0になるという。
この負の偶数におけるゼータ関数0を「自明の零点」と呼ぶ。
全部1/2
リーマン予想とは、
「ゼータ関数の自明でない零点の実部は1/2である」
という予測である。
これは証明された問題ではないけど、以下の事はわかっている。
虚部が小さい方から10兆個の非自明零点の実部は1/2。
実部が1/2 である零点は無限個存在する。
非自明な零点の実部は0より大きく1よりは必ず小さい。
