プランク単位
物理の計算式によく出てくる定数。
c（真空中での光速度）。
G（万有引力定数）。
ħ（ディラック定数）。
C（クーロン力定数）。
k（ボルツマン定数）。
これらの数をすべて1として、考える物理系における単位群を『プランク単位』と言う。
それらは、我々に馴染み深いスケールでなく、物理学の法則に現れる比例定数を基準にしている為、物理的にかなり普遍的だと考えられ、「神の単位」とか、「宇宙の共通単位」とか言われる場合もある（例えば異星人と交流するというテーマで、かつハード寄りのSFを創作するなら、使えるかもしれない）。
一般的なプランクトンとして、とりあえずという感じで、以下の5つが定義される。
プランク時間（T）=約5.39116(13)×10^−44秒
プランク長さ（L）=約1.616229(38)×10^−35m
プランク質量（M）=約2.176470(51)×10^−8kg
プランク電荷（Q）=約1.875545956(41)×10^−18C
プランク温度（Θ）=約1.416808(33)×10^32K
というように、「プランク～」と呼ばれるのは、我々のスケールから見ると、たいていかなり大きいか、小さい。
熱力学の3つの法則
エネルギー保存の法則
滝に水車を設置する。するともちろんガラガラと水車は回ると思う。
つまり、上から勢いよく落ちてくる大量の水が、下の水面を叩きつける際に、水が持つエネルギーのいくらかは、水車の運動エネルギーへと変わる。
例えば水車内部に、磁石が複数、いい具合に配置されてれば、水車が回る事で、その磁気同士の間に、電流が流れる（電磁誘導）。つまり水車の運動エネルギーが、電気エネルギーへと変わる。
「電磁気学」最初の場の理論。電気と磁気の関係 
「電気コンポーネントの動作」直流と交流の使い分け、各デバイスの役割
上記のような流れであれば、「水のポテンシャル→水車の運動→電気」と、エネルギーは変換されていっている。
こういう時、水の元々のエネルギー量を10だとして、水車の運動エネルギーに5変換されたら、水に残るエネルギーは5である。
水車のエネルギーが、さらに2の電気エネルギーに変換されたなら、その時点で、新たなエネルギーなどがよそから追加されてない場合、エネルギー量は、水が5。水車が3。電気が2となる。
つまりエネルギーは変換され、その姿を変えようとも、その量だけは変わらない。これを『エネルギー保存の法則（law of the conservation of energy）』と言う。
アインシュタイン（Albert Einstein。1879～1955）の相対性理論によると、エネルギーと質量は同じ物であるので、エネルギー保存の法則は『質量保存の法則』とも言われる。そしてそれらはまた、『熱力学の第一法則（first law of thermodynamics）』とも言われる。
「特殊相対性理論と一般相対性理論」違いあう感覚で成り立つ宇宙 
エントロピーとは何か。永久機関が不可能な理由。「熱力学三法則」
エントロピー増大の法則
エントロピーとは何か？
これは物事の複雑さとでも言うようなものである。
綺麗に整理整頓された本棚があったとする。もし本棚に収まった大量の本を、適当にバラけさせたなら、本の配置はより複雑になる。
その後、もう一度本を本棚に詰め直す。すると本の配置は再び規則正しくなるが、そのための我々の動きにより発生した、空気や埃の乱れの複雑さは、先程のバラバラの本の複雑さよりも大きくなっている。
このように、どこかの複雑さを整理するには、他のどこかをより複雑にしなければならない。
「タイムトラベルの物理学」理論的には可能か。哲学的未来と過去
言うなれば、エントロピーは増大していくしかない。この事を、『エントロピー増大の法則（law of entropy increase）』と言う。
また、これは『熱力学の第二法則』とも言われる。
絶対零度
熱とは原子の運動の圧力である。
「化学反応の基礎」原子とは何か、分子量は何の量か
仮に原子が動きを一切止めたら、それはつまり熱を持たないに等しい。このような状態は『絶対零度（Absolute zero）』と呼ばれる。
絶対零度には原子の動きはない、そのためにどういう状態で絶対零度になろうとも、その状態は固定されたも同じ。その全く完全な、何かの形を『完全結晶（Perfect crystal）』と言う。
「結晶とはなにか」自然はなぜ簡単に規則正しく存在出来るみたいなのか
明らかであろうが、熱力学第一、第二の法則より、絶対零度でない状態を、絶対零度には出来ない。というような事が『熱力学の第三法則』である。
ブラックホール
事象の地平面と特異点
この宇宙は直感的には、3次元空間と1次元の時間で構成される4次元時空である。
「四次元空間」イメージ不可能、認識不可能、でも近くにある 
「ベクトル空間」基底、次元の定義。線形結合、従属、独立。n次元の写像
一般相対性理論によると、そのような時空を質量は歪ませる。そうして生じる時空の勾配が、物質の進む経路を曲げる。という仕組みで働く力が『重力（gravity）』である。
仮に重力が強すぎて、光すら脱出出来なくなるほどに経路を曲げられたなら、それはもう実質何もかも抜け出せない領域となるはず。特殊相対性理論より、光より速いものは宇宙に存在しないから。
より正確に言うなら、光は常に時空間における測地線（geodesic）を進む。
測地線とは、空間内における、ある位置からある位置までの最短の経路のこと。
「第五公準、平行線問題とは何だったのか」なぜ証明出来なかったのか
しかしそもそも経路がなければ、進む事など出来ない。つまり重力が強すぎて光すら抜け出せないとは、その重力領域の外部へ繋がる経路がひとつも存在しないような状態の事。
そういう強大な重力を生み出す質量の塊を『ブラックホール』。そして、ブラックホールより最も離れた、外部へ続く測地線が存在しない領域、言うなれば万物が脱出不可能な境目を、『事象の地平面（event horizon）』と言う。
「ブラックホール」時間と空間の限界。最も観測不可能な天体の謎
また、ブラックホールの中心は、無限に収縮し続ける点である。そのような点は『特異点』と言われる。
目が悪いといい事
物理学者という人たちはどうも、「直感には反するが」という言い回しが好きすぎるように思う。しかし冷静に考えてみると、直感に反するというのは、全くたいした問題ではない。
例えば目が悪い人なら誰でも、直感なんてものがいかに信用できないかよくわかっているだろう。
これは実際の経験談だが、虫だと思ったら紙切れだったり、なんか象形文字だと思ったら単にアルファベットだったりする事もある。
仮に時空というのが本当に歪んでいたり、量子の存在が本質的に不確定だったりというのが完全に正しい世界観とする。
けどそれはそんなにおかしな事であろうか？
それを直感なんてショボいもので察知出来ないからって、そんなに問題なのであろうか？
「量子論」波動で揺らぐ現実。プランクからシュレーディンガーへ 
「物質構成の素粒子論」エネルギーと場、宇宙空間の簡単なイメージ
ただ非実在性に関しては、さすがにおかしいと言えるのかもしれない。
例えばこの世界が実は4次元空間であるか、1次元であるかなら、まず間違いなく4次元であろう。4次元空間内の3次元空間はありえるだろうが、1次元空間内の3次元など、あっていいはずがない。
しかしそんな考え方（この時空が四次元であるなら、つまりこの時空が四次元以外であると考えられないはず）も、もう古いのかもしれない。
ブラックホールに素粒子を投げ込む
ブラックホールとはどのような天体であるか。
まずそれは『黒体（black body）』というものである。
物理学において黒体とは、光を反射しない物質の事（これは光を発しないという意味ではない）。
「ダークマターとダークエネルギー」宇宙の運命を決めるモノ
太陽のような恒星も黒体と言えばそうである。ただ恒星内部では、原子の振動や衝突により、それらからエネルギーが発生し、外部へ光として放出される。だから恒星は光る。
「太陽と太陽系の惑星」特徴。現象。地球との関わり。生命体の可能性
ブラックホールはどうか。
その外部には光が漏れない。つまりそれは真の黒体なのだろうか？
イスラエルのヤコブ・ベッケンシュタイン（Jacob David Bekenstein。1947～2015）は、何らかの最小の量を、（それは別に何でもいいけど）素粒子として、それをブラックホールに投げ込んだらどうなるかを想像した。
ある空間の中に素粒子が複数あり、空間の温度は絶対零度でないとする。それらの素粒子がどんな状態にあるにせよ、その内ひとつが消えたなら、空間内の質量とエントロピーは下がる。
つまりブラックホールに素粒子を投げ込んだら、ブラックホール外の宇宙全体の質量とエントロピーは下がる。
熱力学の法則を破らないようにするには、素粒子を投げ込んだブラックホールの質量とエントロピーが上がらなければならない。
だが、質量はともかく、ブラックホールのエントロピーとは何か？ それは大きな問題であった。
ブラックホールの熱力学
事象の地平面を越えた時、そこに何があるかを想像するのはあまりに難しい。誰かがそれを知ったとして、多分もうその誰かは、誰にもそれを伝える事が出来ない。
ただ、ここ（ブラックホール内）にエントロピーが存在するならば、熱力学の法則は破られない事になる。
ベッケンスタインの大胆な着想に影響を受けたひとりに、スティーヴン・ホーキング（Stephen William Hawking。1942～2018）がいた。彼は、ブラックホールのエントロピーに関して思考し、ついにはある驚くべき結果を導いた。
それは、以下の式で表されるブラックホールの温度。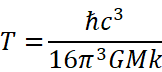
（式の、Tはブラックホールの温度。Mはブラックホールの質量。h、c、π、G、kは定数（プランク定数、光速度、円周率、万有引力定数、ボルツマン定数））
また、ホーキングによると、以下でブラックホールのエントロピーは表す事が出来るという。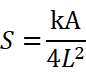
（式のSがブラックホールのエントロピー。Aはブラックホールの表面、つまり事象の地平面の面積。Lはプランク長さ、つまりL^2はプランク面積（物理的意味を持つ最小の面積））
上記の2つの式が示しているのは、ブラックホールの温度は質量が少ないほど高い。そしてエントロピーの大きさは、ブラックホールの表面積から判断出来るという事。
ホーキング放射
ホーキングはさらに驚くべき計算結果も示した。
それは『ホーキング放射（Hawking radiation）』と呼ばれる現象である。
量子効果を考慮に入れると、事象の地平面付近に現れた粒子が崩壊した際に、より細かな粒子が、事象の地平面の外に放出される事があるという。
となると、そのホーキング放射によりブラックホールも、光（エネルギー）を発する天体であるという事を意味する。
そしてそんな事より遥かな問題なのは、それ（ホーキング放射）が実際に起こりうる現象なら、ブラックホールが質量（エネルギー）を失うという事。
ブラックホールはどんどん小さくなり、やがては蒸発する。
この宇宙から消え去る。
ホログラフィック原理とは
ブラックホール情報パラドックス
エントロピーとはそもそも何であるのか。
物事の複雑さは、物事の成立しにくさとも言える。
さらに言うなれば、不明な情報量である。
ではブラックホールに何かを投げ込んだ時に、失われるのは何か？
それは情報に他ならない。
パスワードロックされた金庫を考えてみよう。
パスワードを示唆する物全てと、知ってる人間全員をブラックホールに投げてしまったら、パスワードの情報は失われたも同じ。
もちろん他にも様々な情報が失われるだろう。
ブラックホールがホーキング放射で蒸発するものだとして、放射される粒子群には、かつて失われた情報が残っているだろうか？
エントロピーは、どうなっているだろうか。
ブラックホールという現象に詳しい者は、みなこう考えた。
「全ては戻ってこない。エントロピー（情報）はブラックホールと共に蒸発し、この宇宙から消え去る」
だがその結論は熱力学の法則を崩壊させる。というような問題を、『ブラックホール情報パラドックス（Black hole information paradox）』と言う。
もちろん、ブラックホールという宇宙システムによって消えた情報が、また別の宇宙に新たに現れるという可能性はあろう。そんな事言ったら、この世界がそもそも仮想世界である可能性も、神様がそういうふうに世界を創った可能性もあるわけだが。
「宇宙プログラム説」量子コンピュータのシミュレーションの可能性
世界はホログラム？
情報の最小単位は普通ビットで表される。
「ビットとは何か」情報量の原子は本質的にも原子であるのか
この世界のビットは、何であろう？
ブラックホールは情報を限界まで詰め込んだ領域ではないだろうか？
もしそうならブラックホールのエントロピーが体積でなく、表面積に関係している事は何を意味しているのであろう。その計算式に、微小なプランク面積が含まれる事はいったい何を意味してるのであろう？
単純にこう考えてよかった。まさしくその通り、情報というのは、ある空間領域の表面積に保存される。
しかし、それでは我々はどうなのか？ 我々の臓器、形態、位置、目に見える物、手に触れる物全て。それらはいったい何だというのか？
情報ではないのだろうか？
我々が、情報の投影にすぎないならば問題は解決できよう。
つまり答はこうだ。
ようするに真の情報とは、空間の表面積に保存されるものであり、我々という存在は、表面の情報より内部に映し出されたホログラム映像のようなもの。というような考え方というか、理論が、『ホログラフィック原理（holographic principle）』である。
何が奇妙で、何が奇妙でないか？
そんな事はありえないと思うだろうか？
実際に、そのようだと数学的に厳密に示されているのは、『超ひも理論』か正しいと仮定した場合のみであるという（超ひも理論というのは、最小の物質要素である素粒子ヒモをプランク長さとしているから、最小情報量をプランク単位で表す世界観と合致するのは、直感的にもわかりやすいか）
「超ひも理論、超弦理論」11次元宇宙の謎。実証実験はなぜ難しいか。
ただむしろ、これはそんなに奇妙な事であろうか？
よく考えたら、原子の動きが上手い具合に合わさり、この世界が形成されているというのも、同じくらい奇妙でないだろうか？
ただ、ホログラフィック原理が正しいのだとして、例えば、（量子論を考慮に入れた場合さえ）この世界は連続的に思える。
もし、表面の情報を変換したら、世界は不連続的に急激に変化するのだろうか？
「ループ量子重力理論とは何か」無に浮かぶ空間原子。量子化された時空
なぜ体積でないのか
2つの部屋をくっつけたとしたら、それぞれの部屋に存在していた分子群は、全体としては1つの系となる。この時、分子の数も合計体積も2つの部屋それぞれを合わせたものになるはず。
エントロピーはどうなるか。計算上はエントロピーも2つの部屋に存在していた量が合わさる。
つまり、これだけのことから考えるなら、他の条件（温度とか密度など）が変化しないなら、物理系のエントロピーは体積に比例するはず（2つの部屋がくっついた時の合計エントロピーは、それぞれの部屋の体積を占める合計分子群のエントロピーを合わせたものだから）
ではなぜブラックホールのエントロピーは、そもそもその表面積（より正確には事象の地平面の面積）に比例するのか。
1つの部屋という閉鎖された世界を考える場合、普通は、その内部の分子群が空間中に均一に広がっているものと考えられる。これは特定の部分に強い重力が存在しないことを暗に決めつけている。
だが例えばブラックホールの系のように、物質の密度が非常に高い場合、強力な重力が存在することを考慮に入れて計算しなければならないが、ホーキングらの計算結果はその場合に出てくる。
ホーキングらが見いだしたことは、仮にブラックホールの事象の地平線の面を、一辺の長さがプランク長さの「プランク正方形」を用いて、徹底的に分割させた場合、ブラックホールのエントロピーが、その表面を分けるプランク正方形の個数に等しいこと。とも言える。それぞれのプランク正方形は、エントロピーの最小単位を常に1つ持つ。
当然それは、空間が（情報的に）プランク正方形という基本単位から成り立っていることを思わせる。ホログラフィック原理の背景にもそのような発想がある。
何がこの宇宙のリアルか
バルクと境界面
そもそもホログラムというのは、エッチング（化学薬品などの腐食作用を利用した技法）加工されたプラスチックの二次元片などに、適切なレーザー光線を当てることで、三次元の像を可視化するというテクノロジー。
そして我々が、（自分たちが）生きていると考えている3次元宇宙というのは、実は表面構造の情報が投影されたホログラムのようなものでないだろうか。という説を1990年代のはじめ頃に唱えたのは、ヘラルト・トホーフト（Gerard ‘t Hooft）とレオナルド・サスキンド（Leonard Susskind）だが、この世界観は、その奇妙さから考えると、驚くべきほどに早く広く受け入れられた。この世界観が、ブラックホール情報パラドックスという問題を上手く解決する方法であったことは重要であろう。
宇宙の体積は『バルク（嵩）』と呼ばれることがある。
ホログラフィック原理の世界観が正しいなら、バルクの中でのあらゆる物理学的出来事は、宇宙の表面積（境界面上）で起こることと関連しているはず。
だがそれはつまり、境界面上にコード化された情報が存在しているということなのだろうか。だとすると、我々は本当の意味でホログラフィックな幻影的な存在ということになると思われる。
ループしない宇宙
しかしそもそも、宇宙の境界面とは、いったいどこなのであろう。
ホログラフィック原理の世界観を、無限の宇宙と考える時、境界面が存在しないという自己矛盾が含まれる。だが単にこの宇宙が有限というだけで話を終わらせていいのだろうか。
そもそも従来の宇宙観は、無限の宇宙でないとしても、曲がった次元の幾何学のため（つまり相対性理論的な考え方により）、どこまで行っても結局出発点に戻ってくるというような、つまり球の表面（ただしこの典型的なイメージは、例えば図にする場合、三次元上の二次元として表現されるが、実際の宇宙は三次元空間（例えば四次元の球の表面の三次元空間）と考えられている）のような、とイメージされるのが普通であった。 しかしそのような宇宙は確かに有限ではあるが、おそらく我々が境界面と定義するような部分はない。
プログラムか、アプリケーションか
宇宙の境界面の他に、もう1つ、わかりやすく気になる部分があるだろう。
つまり、この宇宙の三次元空間が幻想であるとは信じがたいほどに、我々がこの三次元の空間の中での物理学を、理解できるし、操作、なんなら支配できると思えるところ。
この制御性と感じていること自体が、幻想だとでもいうのだろうか（もちろんこれは、意識のようなものまでプログラムされた架空の宇宙の住民が、実在の宇宙にどう気づけるのか、というような哲学的問題にも近い）
あるいはこの宇宙にはある種の二重性があるのだろうか。
つまりは、境界面の情報コード（プログラム）、バルク内に投影される出来事（アプリケーション）。この宇宙の物理的出来事（実際この宇宙がどのようなものであれ、そこで起きている変化）をわれわれに理解できるように記述するのに、どちらを参考（基準）にしてもかまわないというような。
実のところ、この二重性の問題に関しての議論は、境界面の問題よりも進んでいると言える。
双対的な異なる物理学
1997年。フアン・マルダセナ（Juan Martín Maldacena）は、 ホログラフィック原理に基づく世界観を、具体的な数学で記述できるような特殊な宇宙の条件を発見した。
その特殊な宇宙とはある種の『反ド・ジッター空間（Anti-de Sitter space。AdSn）』、ようするに、広がった四次元空間に、時間次元が1つ、曲率が均一な負の値をもつような仮想五次元宇宙。また、マルダセナはヒモ理論に必要な、小さくまとまりすぎて見えない次元も考慮に入れていた。
数学的解析によって、まずその宇宙には境界（つまり、内部の体積空間よりも次元が1つ少ない表面と言えるような部分）が認められる。ここまでは、なんてことない話だ（そこまでなら、単に、現実とは違うと思われる高次元宇宙を空想したというだけ）。
だがマルダセナは、この宇宙内部の観測者が認識するであろう物理が、境界上で起こる物理の記述と双対的（つまりは、どちらを利用して考えても、本質的に同じ答、法則が常にでるような、2つの物理学）である可能性を示したのである。
マルダセナの宇宙が、現実の宇宙の形を正確に記述している可能性は低いだろう。しかし、やはり重要なことは、それが技法的に（相対的に）簡単になるような状況を想定した場合、確かに、境界面の構造と、その内部の1次元多い体積構造の物理の関連が示されたこと。
時空間とは何なのか
おそらくマルダセナの示したことは、具体的なホログラム原理宇宙の可能性だけとは言えない。
少なくともマルダセナの想定した宇宙（これはホログラフィック原理を支持する立場から言えば、そうした物理学が存在する特殊宇宙でなく、そのような物理学的実態を計算しやすい宇宙と解釈される宇宙）では、バルクと境界面の物理学は、言うなれば「記述する言語が異なっているだけの同じものの説明」である。
しかし日本語と英語での、一人称の種類とか、同じ記述の別の読みとかいった、片方だけの特色というようなものが、バルクと境界面の物理学にもあるかもしれない。
例えばヒモ理論（重力を含む理論）を前提としているために、バルクの物理には重力が含まれているが、境界面の物理は重力を含まないと考えられている（このことは普通、境界面の物理が、真の意味で我々のリアルの宇宙を記述する物理学ではないはずということを示している。とも言われる）
また、もちろんバルクの物理における次元数は、境界上で定式化される等価の物理の次元よりも高い。つまりこの場合、重力を含まない量子論と、重力を含む空間次元プラス1の量子論が等価でありえることを意味している（現代の我々は、アインシュタインが得た「物体が重力のため落下することは、地面側が同じ加速度で上昇する結果と等価である」という素晴らしい閃きどころか、もっとぶっとんだ等価性を見つけてしまったのだろうか）
だが、ある物理理論を、等価な別の理論へと変換した時、単なるスケール（単位や数値や形）どころか、空間次元そのものの数まで変化してしまうということは、いったい何を意味しているのだろうか。
我々は本質的な時空間というものを見失ってしまったのだろうか。そうでないとしたら、もしかしたら、普通のイメージでおそらくそうあるような、時空間上に存在している物理世界というような世界観から、脱却しなければならないのかもしれない。
はっきり言ってしまうなら、時空の次元はこの宇宙の構成要素の中で、最も基礎的なものではないのかもしれない。まだ我々の気づいていない（いかなる物理法則においても不変的に必要なはずの）土台があるのかもしれない。
境界面物理学の実用性
マルダセナは、境界面上の量子力学理論と、バルク内のヒモ理論の関係の解析より、一方の理論の『結合定数（Coupling constant）』という（例えば素粒子の動作に影響ある）値が小さいなら、もう一方では逆に結合定数が大きくなることも見いだした。
これにはいい面も悪い面もある。
まず、厳密に考えることが難しい物理学の問題に、一般的に用いられる『摂動法（perturbation）』というアプローチ（例えばA、B、Cの三要素が絡むような問題で、まずAのみの場合の答を出してから、BとCを含む場合の変化を加え、修正していくというような方法）がヒモ理論物理においても重要とされているわけだが、 この方法は精度的に、結合定数が大きい場合まったく役に立たないとされている。つまり、境界面上理論とバルク内理論は常にどちらかの計算が非常に難しく、結果的に（両方の答を出して、合ってるか確かめるという単純な方法が使いにくく）等価性を確認することが困難。これはあまり嬉しい話ではない。
しかし一方で、結合定数の大小の変化は、一方の理論で（結合定数のために）難しかった問題が、もう一方の理論では比較的簡単になることを意味している。
実際例えば、粒子加速器の実験などで生じる素粒子群の影響を、場の量子論（量子色力学）で記述する場合などに、結合定数の値が大きくて摂動法の正確さが失われることがある。そういう時、実験がバルク内でなく、境界面上で行われていると仮定し、つまりは（等価と考えられるが、計算は簡単になっている）境界面上物理を用いて計算し、実験結果データと近しい計算結果を得る。というような実用的な使い方が、ある程度成功もしているという。
境界面の物理理論は、（たとえそれがリアルな宇宙をありのまま記述するようなものではないとしても）物理計算の道具（技巧）として、少なくとも実用的なようである。
